Proszę o pomoc betka: W okrąg o promieniu r wpisano kwadrat i na tym samym okręgu opisano trójkąt równoboczny. Oblicz długość promienia okręgu, wiedząc że suma długości boku kwadratu i boku trójkąta równobocznego jest równa 12.

Christopher: Rozwiąż na R układ równań

	0,5a		c2		c3
R=		& a+c=12 &		sin60=
	cos45		2		4R

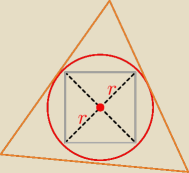
think: przekątna kwadratu to średnica okręgu 4a + 3b = 12 d = a√2

	d		a√2
r =		=
	2		2

Teraz z własności okręgu wpisanego w trójkąt:

	2P		a2√3   2*   4
r =		=co dla trójkąta równobocznego przybiera postać:		=
	a + b + c		3b

	a2√3
	6b

mamy taki układ równań 4a + 3b = 12

a√2		a2√3
	=
2		6b

którego rozwiązanie już pozostawiam Tobie...

think: ale gaf, ślepa komenda ze mnie o poranku tam jest warunek a + b = 12 nie 4a + 3b = 12