marta: Zad.1 Środki kolejnych boków trapezu równoramiennego połączono odcinkami. Udowodnij, że suma pól powstałych 4 trójkatów jest równa polu powstałego czworokąta. Zad.2 udowodnij, że jeśli ab< 0 i a+b nie jest równe 0, to:

a		b
	+		< −2
b		a

Jack: 2.

a		b
	+		<−2
b		a

a2		b2
	+		<−2
ab		ab

(a+b)2−2ab
	<−2
ab

(a+b)2		−2ab
	+		<−2
ab		ab

(a+b)2
	−2<−2
ab

(a+b)2
	<0
ab

ab<0 oraz (a+b)²>0 więc wszystko gra. Kroki są równoważne a ostatni wynika bezpośrednio z założeń.

Bogdan:

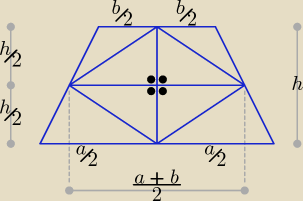
	a + b
Pole trapezu PTR =		* h
	2

	1		a + b		a + b		1
Pole czworokąta PCZW =		*		* h =		* h =		PTR
	2		2		4		2

Czworokąt jest rombem Suma pól trójkątów

	a + b		a + b		a + b
PΔ = PTR − PCZW =		* h −		* h =		* h = PCZW
	2		4		4