geometria dowód Mimi: Udowodnić, że jeżeli P jest punktem wewnętrznym trójkata ABC, to suma odległości punktu P od wierzchołków A,B, C jest większa od połowy obwodu danego trójkata.

Mimi: Pomoże ktoś

Godzio: zaraz się pomyśli

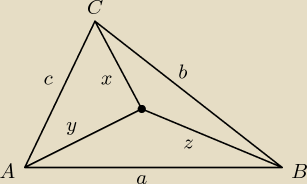
Godzio: Z warunku istnienia trójkątów mamy takie nierówności (po jednej z każdego) x + y > c z + y > a x + z > b sumując je otrzymamy: x + y + z + y + x + z > c + a + b 2x + 2y + 2z > a + b + c /:2

	a + b + c
x + y + z >		c.n.d.
	2

Jak czegoś nie rozumiesz to pisz

runny: Z nierówności trójkąta mamy: d + e > a e + f > b f + d > c Dodajemy nierówności stronami d + e + e + f + f + d > a + b + c 2d + 2e + 2f > a + b + c 2(d + e + f) > a + b + c

	a + b + c
d + e + f >
	2

c.n.d.

Mimi: dzięki rozumiem. Nie przepadam za dowodami.

Christopher:

	a+b+c
Można również wykazać,że		=d2 (cosβ1 + cosβ2) + e2 (cosγ1 +
	2

cosγ₂) + ^f₂ (cosα₁ +cosα₂) α=α₁ + α₂ , β=β₁ + β₂ ,γ=γ₁ +γ₂ ,gdzie α,β,γ − kąty Δ ABC

	a+b+c
I teraz		= d + e + f ⇔ α1 ,α2,β1,β2,γ1,γ2 = 0
	2

	a+b+c
Ale suma tych kątów musi wynosić 180,a zatem		< d+e+f
	2

Ale sposób Runny prostszy,a zatem lepszy