f
Maciek:
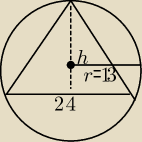
Oblicz pole trójkąta .
Czyli mamy 1/2 a*h . I tu pytanie jak wyliczyć h?
3 paź 22:40
think: może należy skorzystać ze wzoru na trójkąt wpisany w okrąg?
3 paź 22:51
think: przy czym α to kąt naprzeciw boku którego długość znasz

3 paź 22:52
runny:
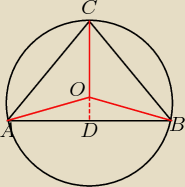
Czerwone odcinki to promienie
ΔAOB jest równoramienny, stąd jego wysokość dzieli podstawy na połowy
Czyli ΔADO jest prostokątny, jedna z jego przyprostokątnych równa jest 12, a przeciwprostokątna
równa jest 13. Stąd |DO| = 5 (Pitagoras). |CO| + |OD| = 13 + 5 = 18
3 paź 22:54
think: no dobra runny niewątpliwie Twój sposób jest szybszy, więc czuję się znokautowana

także
zmykam spać

dobrej nocy i do następnego starcia

3 paź 22:58
Eta:
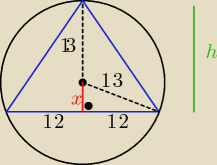
czy w treści zad. jest,że trójkąt jest równoramienny? ( bo nie napisałeś)
jeżeli równoramienny , to:
h= x+r
x
2= 13
2 − 12
2=.........
P= .......
3 paź 23:01
Maciek: dzięki

3 paź 23:01
think: Eta a czy to nie jest hmm wniosek z tego że środek okręgu leży na linii wysokości?
3 paź 23:03
think: 
dobra już dobra miałam iść to idę

3 paź 23:04
Eta:
Hehe

....... skąd mam wiedzieć,czy rysunek( bohomaz)
podany przez Maćka jest prawidłowy

3 paź 23:05
Bogdan:
 Maciek
Maciek podał tylko rysunek, brak treści zadania. Nie można na podstawie rysunku
Maćka
przyjąć, że |CD| = 18.
Chodzi mi o rzetelne podawanie treści zadania przez oczekujących pomocy.
3 paź 23:07
Eta:

3 paź 23:08
runny: Gdyby nie był równoramienny zadanie byłoby tylko
trochę trudniejsze

3 paź 23:09
Maciek:
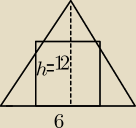
a tutaj jak obliczyć pole kwadratu?
3 paź 23:11
Maciek: tak trójkąt jest równoramienny

3 paź 23:12
Maciek: w drugim zad też
3 paź 23:13
Eta:
Oczekujesz poprawnego rozwiązania?
Napisz poprawną treść zadania

3 paź 23:13
runny: 6 to podstawa trójkąta, czy bok kwadratu?
3 paź 23:13
runny: ok, cofam. Gdyby 6 było bok kwadratu, to zadanie byłoby trochę za proste

3 paź 23:14
Maciek: w trójkąt równoramienny o podstawie 6 i h+12 wpisano kwadrat którego 2 wierzchołki lezą na
podstawie a pozostałe na ramionach . OBLICZ POLE KWADRATU
3 paź 23:14
Maciek: * h =12
3 paź 23:15
runny: Trzeba skorzystać z podobieństwa trójkątów, a potem rozwiązać równanie kwadratowe.
3 paź 23:16
Maciek: czyli jak zacząć najprościej ?
3 paź 23:17
runny: phi, nawet nie kwadratowe

P = 16
3 paź 23:18
Maciek: jak to rozpisać?
3 paź 23:18
runny:
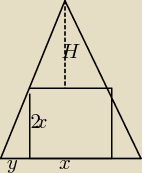
Z podobieństwa:
stąd:
H = {2x
2}{y}
No i teraz mamy
H + 2x = 12
2x + 2y =6
rozwiąż
3 paź 23:20
runny: *
x − połowa boku kwadratu
3 paź 23:20
Eta:
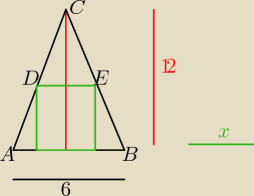
x−−− dł. boku kwadratu, x >0
ΔABC ~ ΔDEC
x=..........
3 paź 23:22
 Oblicz pole trójkąta .
Czyli mamy 1/2 a*h . I tu pytanie jak wyliczyć h?
Oblicz pole trójkąta .
Czyli mamy 1/2 a*h . I tu pytanie jak wyliczyć h?

 Czerwone odcinki to promienie
ΔAOB jest równoramienny, stąd jego wysokość dzieli podstawy na połowy
Czyli ΔADO jest prostokątny, jedna z jego przyprostokątnych równa jest 12, a przeciwprostokątna
równa jest 13. Stąd |DO| = 5 (Pitagoras). |CO| + |OD| = 13 + 5 = 18
Czerwone odcinki to promienie
ΔAOB jest równoramienny, stąd jego wysokość dzieli podstawy na połowy
Czyli ΔADO jest prostokątny, jedna z jego przyprostokątnych równa jest 12, a przeciwprostokątna
równa jest 13. Stąd |DO| = 5 (Pitagoras). |CO| + |OD| = 13 + 5 = 18
 także
zmykam spać
także
zmykam spać  dobrej nocy i do następnego starcia
dobrej nocy i do następnego starcia 
 czy w treści zad. jest,że trójkąt jest równoramienny? ( bo nie napisałeś)
jeżeli równoramienny , to:
h= x+r
x2= 132 − 122=.........
P= .......
czy w treści zad. jest,że trójkąt jest równoramienny? ( bo nie napisałeś)
jeżeli równoramienny , to:
h= x+r
x2= 132 − 122=.........
P= .......

 dobra już dobra miałam iść to idę
dobra już dobra miałam iść to idę 
 ....... skąd mam wiedzieć,czy rysunek( bohomaz)
podany przez Maćka jest prawidłowy
....... skąd mam wiedzieć,czy rysunek( bohomaz)
podany przez Maćka jest prawidłowy 
 Maciek podał tylko rysunek, brak treści zadania. Nie można na podstawie rysunku Maćka
przyjąć, że |CD| = 18.
Chodzi mi o rzetelne podawanie treści zadania przez oczekujących pomocy.
Maciek podał tylko rysunek, brak treści zadania. Nie można na podstawie rysunku Maćka
przyjąć, że |CD| = 18.
Chodzi mi o rzetelne podawanie treści zadania przez oczekujących pomocy.


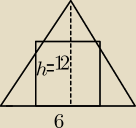 a tutaj jak obliczyć pole kwadratu?
a tutaj jak obliczyć pole kwadratu?



 P = 16
P = 16
 Z podobieństwa:
Z podobieństwa:
 x−−− dł. boku kwadratu, x >0
ΔABC ~ ΔDEC
x−−− dł. boku kwadratu, x >0
ΔABC ~ ΔDEC