W trójkącie równoramiennym ABC mamy |AC|=|BC|=4p{3}. smmileey: W trójkącie równoramiennym ABC mamy |AC|=|BC|=4√3. Wysokość opuszczona na podstawę trójkąta jest równa odcinkowi łączącemu środek podstawy z środkiem ramienia trójkąta. Oblicz różnicę między długością promienia R okręgu opisanego na trójkącie, a promieniem r okręgu wpisanego w ten trójkąt. Jedyne co udało mi się zauważyć, to że odcinek łączący środek podstawy ze środkiem ramienia trójkąta jest równy połowie ramienia trójkąta. Nie wiem co robić dalej. Proszę o pomoc.

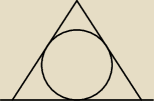
M.: Nazwij sobie C Δ A B Oraz punkty przecięcia z okręgiem: na boku AB D, na BC E i na CA F Zgodnie z zasadą o równości odcinków stycznych: BD=BE CE=CF AF=AD Zauważ więc,że wszystkie boki są sobie równe. Trójkąt jest równoboczny. r=1/3 wysokości trójkąta równobocznego R=2/3 wysokości

smmileey:

	2√3		4√3
Z tego co piszesz wynika, że r=		, a R =		, czyli różnica
	3		3

	2√3
R−r=
	3

W odpowiedziach podają 10√3 − 12.