Pole trójkąta prostokątnego o kącie ostrym α jest równe P. Oblicz promień R koła smmileey: Pole trójkąta prostokątnego o kącie ostrym α jest równe P. Oblicz promień R koła opisanego na tym trójkącie. Nie mam na to pomysłu, proszę o pomoc.

smmileey: Krystian, pisz to szybciej

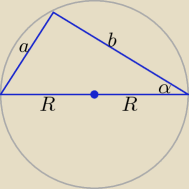
Pani Ł.: Zrób sobie rysunek: a,b − przyprostokątne, c − przeciwprostokątna c²=a²+b² 1/2ab=P => a=2P/b sinα=b/c => b=csinα c²=a²+b² c² = (2P/b)²+(csinα)² c² = (2P/csinα)²+(csinα)² c² = 4P²/c²sin²α+c²sin²α ....

	4P2
c4=
	sin2α−sin4α

	4P2
c4=
	sin2αcos2α

	2P
c=√
	sinαcosα

	2Psinα
b=sinα*c=√
	cosα

	2P		2Pcosα
a=		=√
	b		sinα

	P
R=abc/4P=√
	sin2α

Bogdan:

a
	= sinα ⇒ a = 2Rsinα
2R

b
	= cosα ⇒ b = 2Rcosα
2R

	1
Pole P =		*2Rsinα*2Rcosα ⇒ P = R2sin2α ⇒ R = √ P / sin2α
	2

smmileey: świetnie, oba świetnie, Bogdan widzę się wiele nie oliczył

Eta:

	a*b
P=
	2

c= 2R ze wzoru sinusów

	b
		= 2R => b= 2R* cosα
	sinβ

bo: sinβ= cosα

	b*c
P=		*sinα
	2

	2Rcosα*2R*sinα
P=
	2

P= 2R²sinα*cosα , 2sinα*cosα= sin2α P= R²*sin2α

	P
R= √
	sin2α

smmileey: Eta, też mi się podoba, tyle, że jeszcze nie było wzoru sinusów u nas