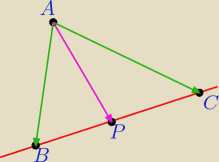
Wektory Dwiekropki: Proszę o jakąś podpowiedź. Dane są 3 niewspółliniowe pkt A, B i C oraz okt P leżący na prostej BC. Wyznacz wektor Ap za pomocą wekt AB i AC nie będę pisała strzałek nad wektorami bo za dużo pracy.. Oto moje rozwiązanie.. AP= ?AB + ?AC a więc: AP=AB+BP i jednoczesnie AP=AC+CP i dodajemy te r−nia stronami: 2AP=AB+AC+BP+CP teraz trzeba pozbyć się BP+CP więc: BP= AP−AB CP= AP−AC Podtsawiamy do wczesniejszego r−nia i wychodzi: 2AP=AB+AC+AP−AB+AP−AC 0=0 CZYLI MASŁO MAŚLANE.. ; / Proszę o jakąś podpowiedź.

Jack: AP=AB + AC ?

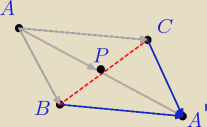
Jack: Zauważ, że |AA'|=2|AP| oraz że, wektor AA'= wektor AB + wektor AC

Dwiekropki: tam są znaki zapytania.. czyli że AP= cośAB+cośAC ..zaraz będę kombinować czy coś wyjdzie.. : ) dziękuję.

Jack: ok powodzenia!

Dwiekropki: Ale momencik..! Przecież P nie musi być w połowie BC.. tylko to jest dowolny punkt.. i jeśli narysujemy nie w połowie BC to nie wyjdzie już równoległobok ..