Na osi OX znajdź taki punkt P, aby pole trójkąta ABP było=8 Lukas: Dane są punkty A=(3,2) i B=(5,2). Na osi OX znajdź taki punkt P, aby pole trójkąta ABP było równe 8.

ce es: wzór herona + wzór na długość odcinka w ukladzie współrzędnych koniec.

ce es: Wzór herona P = √p(p−a)(p−b)(p−c) gdzie p = połowa obwodu

Jack: miałeś już wyznaczniki Lukas?

Lukas: to znaczy? bo pierwszy raz słyszę o wzorze herona Czy jest jakaś prostsza metoda? Pozdrawiam

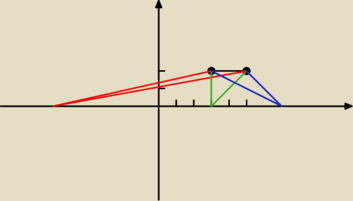
Godzio: Moim zdaniem nie ma takiego punktu, bo wysokość musiałaby się równać 16 a tu widać że nigdy tak nie będzie

Lukas: przepraszam B=(−2,4)....

Lukas: problem w tym, że dalej nie wiem jak to rozwiązać...