okrąg wpisany, opisany Patrycja: W okrąg wpisano trójką ABC. Przez wierzchołek A poprowadzono styczną do okręgu, a następnie poprowadzono równoległą do tej stycznej, przecinającą boli AB i AC odpowiednio w punktach D i E. Wykazać, że na czworokącie BCDE mozna opisać okrąg. Można gdy suma przeciwległych wierzchołków tego czworokąta wypukłego wynosi 180 stopni. Ktoś pomoże?

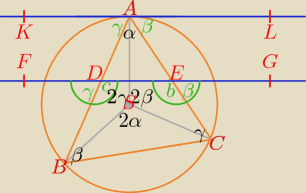
Bogdan: S − środek okręgu, ∡BDE = c, ∡CED = b. Korzystamy z twierdzeń: 1) o kącie wpisanym i środkowym opartych o ten sam łuk okręgu (np. ∡BAC i ∡BSC); 2) o kącie dopisanym i środkowym opartych o ten sam łuk okręgu (np. ∡BAK i ∡BSA); 3) o dwóch prostych równoległych przeciętych trzecią prostą i kątach odpowiadających (np. ∡DAK i ∡BDF); 4) o kątach przyległych (np. ∡BDF i ∡BDE): c = 180^o − γ oraz b = 180^o − β 5) o okręgu opisanym na czworokącie.

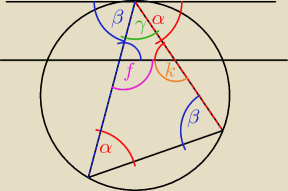
Patrycja : α+β+γ=180 f+β=180 β=180−α−γ f+180−α−γ=180 f−α−γ=0 f=α+γ k+α=180 α=180−β−γ k+180−β−γ=180 k−β−γ=0 k=β+γ f+β=α+γ+β=180 k+α=β+γ+α=180 co należało wykazać. Dziękuję Bogdan. Pomogłeś.