Oblicz tg kąta nachyenia xxxxxxxxxxxxxxxxxxxxxxxxxxxxxx: Dany jest ostroslup prawidlowy czworokatny o podstawie ABCD i wierzcholku S, w ktorym |AS| = 3/2|AB|. Na odcinkach BS i DS obrano odpowiednie punkty E i F tak ze |ES| = 2|BE|, |FS|=2|DF|. Przez punkty A, E, F poprowadzono płaszczyzne. Oblicz tg kata nachylenia przekroju do plaszczyzny podstawy ostroslupa. Oznaczylem krawedz podstawy AB =x, SE=2a, BE=a, uzaleznilem wszystko od x.

	x√3
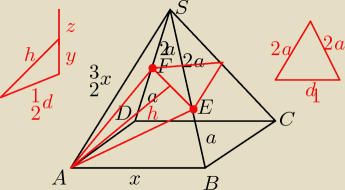
Przekrojem jest deltoid. Jedna z Krawedzi deltoidu − czyli AE=		, wysokosc tego
	2

	x√7
ostroslupa		. I nie wiem co dalej?
	2

xxxxxxxxxxxxxxxxxxxxxxxxxxxxxx:

	√14
Odp.
	6

Godzio: d = x√2

3
	x = 3a ⇒ x = 2a
2

z + y = H

	1
H2 + (		d)2 = 9a2
	2

	1		1
H2 = 9a2 −		* x2 * 2= 9a2 −		* 4a2 * 2
	4		4

H² = 9a² − 2a² H = √7a Z podobieństwa liczę podstawie trójkąta :

d1		2a
	=
d		3a

d1		2
	=
x√2		3

	4
d1 =		a√2
	3

Wysokość trójkąta ( tego po prawej na czerwono)

	1
z2 + (		d1)2 = 4a2
	2

	1		16
z2 +		*		a2 = 4a2
	2		9

	2√7
po obliczeniu: z =		a
	3

	2√7		3√7a − 2√7a		√7a
y = H − z = √7a −		a =		=
	3		3		3

	y		√7a     3		√7		√14
tgα =		=		=		=
	1   d 2		a√2		3√2		6