Rozwiąż metoda algebraiczna i graficzną
Kamila: |x + 1| + |x +3| = 4
2 paź 15:34
Kamila: proszę o pomoc

2 paź 15:52
mika: Nie wiem czy dobrze pamiętam,
określasz dziedzinę, czyli w tym przypadku
D=R\{−3,−1}
musisz rozważyć 4 przypadki, czyli 4 układy:
1. x+1 ≥ 0
x+3 ≥ 0
2. x+1 < 0
x+3 < 0
3. x+1 ≥ 0
x+3 < 0
4. x+1 < 0
x+3 ≥ 0
z każdego liczysz część wspólną i odpowiedno podstawiasz do równania. jeżeli jest ≥ 0 to nie
zmieniasz znaku, jeżeli jest < 0 to zmieniasz znak.
i mając do rozwiązania 4 równania − rozwiązujesz je

i potem sumujesz wszystkie 4 wyniki, tylko uważnie sprawdź czy przypadkiem któryś nie jest poza
dziedziną − są dwie liczby które nie należą do dziedziny −3 lub −1
2 paź 15:54
runny: Nie do końca
Dziedziną jest zbiór liczb rzeczywistych (x ∊ ℛ)
Rozpatrujemy trzy przypadki:
1o x ∊ (−∞ ; −3)
2o x ∊ <−3 ; −1)
3o x ∊ <−1 ; ∞)
Podstawiasz dowolną liczbę z danego przedziału, który aktualnie rozpatrujesz do wartości
bezwzględnej. Jeśli wynik ujemny wartość opuszczasz z minusem, jeżeli dodatni to z plusem.
Patrzysz jaki wyszedł x, jeżeli należy do rozpatrywanego zakresu to jest on wynikiem, jeżeli
nie to go odrzucamy.
2 paź 16:07
mika: mi się wydaje, że (x ∊ ℛ) ale bez {−3,−1}
dlatego napisałam D=R\{−3,−1}.
2 paź 16:13
runny: Wartość bezwzględna jest określona dla zera i wynosi |0| = 0.
Nie ma powodu, aby wykluczać z dziedziny x, dla których wartość bezwzględna się zeruje.
2 paź 16:14
mika: ale przy tych liczbach po podstawieniu i tak wyjdzie sprzeczność, więc one tego nie spełniają

2 paź 16:33
runny: Co nie znaczy, że są wyłączone z dziedziny.
2 paź 16:37
mika: no doobra. pozdrawiam

2 paź 16:40
Kamila: dzięki wielkie! a metoda graficzna? jak zrobić to na wykresie? pozdrawiam !
2 paź 17:36
Godzio:
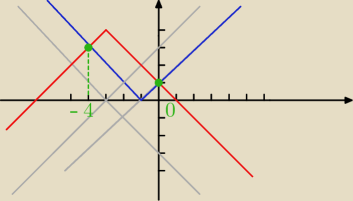
|x + 1| = 4 − |x + 3|
|x + 1| =
− |x + 3| + 4
2 paź 17:41

 i potem sumujesz wszystkie 4 wyniki, tylko uważnie sprawdź czy przypadkiem któryś nie jest poza
dziedziną − są dwie liczby które nie należą do dziedziny −3 lub −1
i potem sumujesz wszystkie 4 wyniki, tylko uważnie sprawdź czy przypadkiem któryś nie jest poza
dziedziną − są dwie liczby które nie należą do dziedziny −3 lub −1


 |x + 1| = 4 − |x + 3|
|x + 1| = − |x + 3| + 4
|x + 1| = 4 − |x + 3|
|x + 1| = − |x + 3| + 4