Twierdzenie cosinusów lemurek: Twierdzenie cosinusów mam problem z jednym zadaniem

	1+2√7		√33
Prawidłowy wynik to		, a mi wychodzi
	3		3

Może ktoś spojrzeć, bo nie wiem co robie źle

	2√2
W trójkącie ostrokątnym dane są a=2 cm i b=1cm oraz sinα=		. Oblicz c.
	3

Godzio: podaj całą treść...

lemurek: Takie zadania mam właśnie w zbiorze... Rozmieszczenie katów i boków każą wziąć z księżyca

Godzio: α∊(0,90)

	8		1
cos2α = 1 −		=
	9		9

	1
cosα =
	3

1^o

	8c
1 = 4 + c2 −		−− z tego otrzymasz sprzeczność i
	3

2^o

	4
c2 = 4 + 1 −
	3

	11
c2 =
	3

	√33
c =
	3

3^o

	2c
4 = 1 + c2 −
	3

	2
0 = c2 −		c − 3
	3

0 = 3c² − 2c − 9 Δ = 4 + 108 = 112 √Δ = 4√7

	2 + 4√7		1 + 2√7
c1 =		=
	6		3

	2 − 4√7		1 − 2√7
c2 =		=		−−− odrzucamy bo bok nie może byćujemny
	6		3

lemurek: Dzięki...

Godzio:

	√33
Tak się zastanawiam dlaczego odrzucili c =		hmmm
	3

lemurek: Może po prostu błąd w odpowiedziach Nie znajduję żadnego innego wytłumaczenia

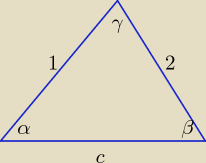Bogdan: Proponuję takie rozwiązanie:

	2√2		1
sinα =		, cosα =
	3		3

Z twierdzenia sinusów:

2		1		1		√2		√7
	=		⇒ sinβ =		sinα =		, cosβ =
sinα		sinβ		2		3		3

sinγ = sin(180^o − (α + β)) = sin(α + β) = sinα cosβ + sinβ cosα =

	2√2		√7		√2		1		√2(2√7 + 1)
=		*		+		*		=
	3		3		3		3		9

Jeszcze raz z twierdzenia sinusów:

2		c
	=		⇒
sinα		sinγ

	sinγ		√2(2√7 + 1)   9		2√7 + 1
⇒ c = 2*		= 2*		=
	sinα		2√2     3		3

think: nie wiem czy to nie ma związku z tym, że najczęściej kąty nazywa się tak, że α leży naprzeciw boku a, β naprzeciw b i γ naprzeciw c. Tak jak to Bogdan umieścił na rysunku. Wy rozpatrzyliście po prostu wszystkie możliwe położenia α a ona ma to jedno.

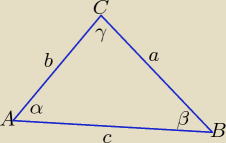Bogdan: Masz rację think, tak właśnie zawsze oznacza się elementy trójkąta. Niewłaściwe oznaczenia to jeden z najpowszechniejszych grzechów.