trapez w okręgu mike93: W okrąg wpisano trapez równoramienny o podstawach równych 12 i 8 oraz ramionach równych √40. Oblicz długość promienia. Doszedłem do tego że wysokość jest równa 6 a dalej nic nie wymyśliłem. Pomóżcie proszę.

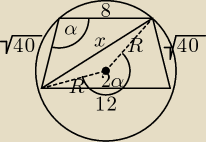
think: no to chyba mam jest coś takiego jak tw. Ptolemeusza : "Jeżeli czworokąt jest wpisany w okrąg, to iloczyn długości jego przekątnych jest równy sumie iloczynów długości boków przeciwległych" ponieważ przekątne są równe w trapezie równoramiennym, to x−oznacza długość takiej przekątnej x*x = 8*12+ √40*√40 = 96 + 40 = 136 x² = 136 x = 2√34 musisz wyznaczyć miarę kąta α i skorzystać z tw. cosinusów x² = R² + R² − 2R*Rcos(2π − 2α)

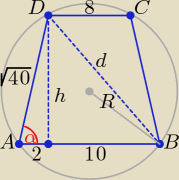Bogdan: h = √40 − 4 = 6 d = √36 + 100 = √136

	6
sinα =
	√40

	d
Na podstawie twierdzenia sinusów dla trójkąta ABD: R =
	2sinα

think: także do koloru do wyboru tw sinusów albo cosinusów, co Ci bardziej na rękę