ZW Dwiekropki: Czy ktoś na chłopski rozum wytłumaczyć by mi mógł czym się różni przeciwdziedzina od ZW..?! Bo chyba nigdzie nie ma tego napisane.. mnóstwo książek przejrzałam i stron internetowych.. ale wszytko jest okropnie zapisane.. ; / a poza tym co to jest suriekcja.. mam def przed sobą, ale nie jest ona zbyt 'czytelna' ..

Dwiekropki: Chyba ostatnio zadaje za trudne pyt bo nikt mi nie odpowiada..

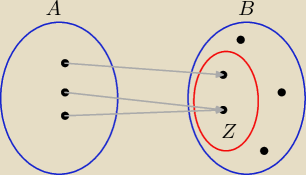
Bogdan: A to dziedzina funkcji B to przeciwdziedzina funkcji Z to zbiór wartości funkcji Tu mamy odwzorowanie zbioru A w zbiór B, jest to odwzorowanie typu w Jeśli Z = B to jest odwzorowanie typu na Za chwilę odpowiem na następne pytanie.

Dwiekropki: Rozumiem, ze ZW musi być zawsze zawarty w przeciwdziedzinie..? Bo injekcja to f−cja po prostu roznowartosciowa np y=x+2 tak..? A dla suriekcji jaki mozna podac przykład..?

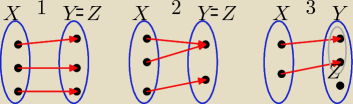
Bogdan: X − dziedzina, Y − przeciwdziedzina, Z − zbiór wartości funkcji 1. BIJEKCJA − funkcja różnowartościowa, odwzorowanie typu na 2. SURIEKCJA − funkcja nie jest różnowartościowa, odwzorowanie typu na 3. INIEKCJA − funkcja różnowartościowa, odwzorowanie typu w

Dwiekropki: znalazłam przykład y=x³ ale dlaczego tak jest to nie mam pojęcia niestety..

Dwiekropki: Ok.. czyli x³ jest różnowartościowa.. ale jak spr jest suriekcją..? jakies obliczenia? ciezko mi sobie to wyobrazic.. wiem jak wyglada ta funkcja.. rysunki tez rozumiem.. ale jakbym miala sprawdzic czy f−cja jest suriekcją to nie mam poj ęcia jak to zrobić..

Bogdan: Określ funkcję: jest różnowartościowa, nie jest różnowartościowa. Wyznacz jej dziedzinę X, przeciwdziedzinę Y, zbiór wartości funkcji Z. Dopasuj odpowiedzi do jednego z podanych wyżej przypadków: bijekcja, suriekcja, iniekcja.

Dwiekropki: Wszystko rozumiem.. ale jak mam okreslic ZW a jak Y skoro dla mnie jedno i drugie zawsze bylo tym samym..?

Dwiekropki: Tzn, nie wszytko rozumiem skoro zadaje tak głupie pytania..

Dwiekropki: Przeczytałam, że dowolna funkcja jest suriekcją, jeśli jako zbiór Y przyjmiemy jej ZW.. juz wiem cos wiecej..

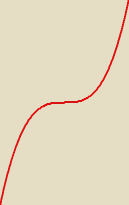
Witek: Tak sobie spróbuję pyknąć to zadanko bo się uczę tego właśnie(Mogą być błędy!) Mamy x³. Widac z wykresu, że zachodzi: f(x1)=f(x2)=>x1=x2 czyli "zastrzyk"−iniekcja jest. Można też zauważyć, że cały zbiór wartości pokrywa się z przeciwdziedziną. Jest to odwzorowanie "na" (Tutaj mam pytanie czy jest to automorfizm. Tak mi sie wydaje, bo przechodzi przez (0,0) czyli jest liniowe i jest typem R−−−−>R) Jednym słowem BIJEKCJA Pozdrawiam

rob: 1/(x²+1)

rob: sqrt{1−x²}

rob: a) X=Y=R, b) X=Y=R z zerem to injekcje? surjekcje? jak musi się zmienić X i Y, żeby były bijekcjami?

rob: dokładniej: a) y=1/(x²+1) b) y=√1−x²

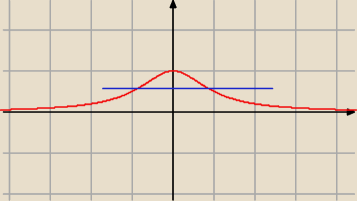
Aga1.: Funkcja y=1/(x²+1) nie jest różnowartościowa (pokazuje niebieska prosta) i nie jest typu na. ZW=(0,1> Przeciwdziedzina =R (0,1>⊂R

Cichy: Dlaczego przeciwdziedzina = R

Pytacz: Czy przeciwdziedzina zawsze = R? A jak nie, to np. kiedy jest inna?

Pan Kalafior: F(f) = f' F→E D = { f:R→R : f jest różniczkowalna }, E = { f : f jest ciągła } Czy E = R ?