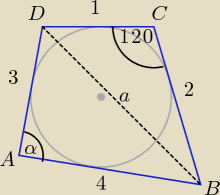
czworaokąt utrecht: oblicz pole czworokąta ABCD oraz promień okręgu wpisanego w tenże czworokąt, mając dane: |AB| = 4 |BC| = 2 |CD| = 1 |AD| = 3; oraz miarę kąta BCD = 120'

utrecht: pomoze ktos?

Bogdan: |BD| = a, cos120^o = −0,5, sin120^o = √3/2 Z twierdzenia cosinusów w trójkącie BCD: a² = 1 + 4 − 2*1*2*(−0,5) = 7

	3
Z twierdzenia cosinusów w trójkącie BDA: 7 = 9 + 16 − 2*3*4*cosα ⇒ cosα =
	4

	9		7		√7
sin2α = 1 −		=		⇒ sinα =
	16		16		4

Pole czworokąta ABCD:

	1		1
P = PBCD + PBDA =		*1*2*sin120o +		*3*4*sinα = .....
	2		2

Bogdan: Pole powierzchni dowolnego wielokąta opisanego na okręgu można wyznaczyć z zależności: P = p * r, gdzie p to liczba równa połowie długości obwodu wielokąta, r to długość promienia okręgu wpisanego w wielokąt.

	P
Stąd r =
	p

utrecht: dziekuje bardzo !