 a = 8
PABC/PDBE = 32
Jeśli spojrzysz na rysunek wynika z niego, że Δ DBE jest trójkątem, którego kąt B = 60 st.,
więc
kąt E = 90 st. Czyli ΔDBE jest prostokątny.
PABC= a2p(3)/4
PABC= 82p(3)/4 = 16p(3)
16p(3)/PDBE = 32
32 * PDBE= 16p(3)
PDBE = p(3)/2
z trójkąta DBE − pole
DE * EB / 2 = p(3)/2
tg B = tg 60 st = DE/EB = p(3)
p(3) = DE/EB
DE = p(3) * EB
wracamy do:
DE * EB / 2 = p(3)/2
p(3) * EB * EB / 2 = p(3)/2
EB * EB = 1
stąd EB = 1
a = 8
PABC/PDBE = 32
Jeśli spojrzysz na rysunek wynika z niego, że Δ DBE jest trójkątem, którego kąt B = 60 st.,
więc
kąt E = 90 st. Czyli ΔDBE jest prostokątny.
PABC= a2p(3)/4
PABC= 82p(3)/4 = 16p(3)
16p(3)/PDBE = 32
32 * PDBE= 16p(3)
PDBE = p(3)/2
z trójkąta DBE − pole
DE * EB / 2 = p(3)/2
tg B = tg 60 st = DE/EB = p(3)
p(3) = DE/EB
DE = p(3) * EB
wracamy do:
DE * EB / 2 = p(3)/2
p(3) * EB * EB / 2 = p(3)/2
EB * EB = 1
stąd EB = 1
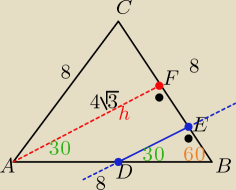 P(ΔABC)= 16√3 to P(ΔABF)= 8√3
P(ΔABC)= 16√3 to P(ΔABF)= 8√3
| 16√3 | √3 | |||
P(ΔDBE)= | = | |||
| 32 | 2 |
| P(ΔAFB) | |
= k2
| |
| P(ΔDBE) |
| 8√3 | |||||||
= k2 = 16 ...... => k=4
| |||||||
|
| 1 | 1 | |||
|DE| = | *|AF| = | *4√3
| ||
| 4 | 4 |