jednokładność. mambaxD: Proszę o sprawdzenie! Treść jest następująca: Dany jest odcinek o końcach A(2,4) i B(4,−2) oraz punkty O(0,0) i S(−2,−1). Narysuj figurę, która jest obrazem odcinka AB w podanej jednokładności. Wyznacz współrzędne odpowiednich punktów. a) J²_o i robię to tak.. → → 1. J²_o (A)=A' ⇔ OA' = 2 OA A' ( x' , y' ) [x'−0; y'−0] = 2[2−0; 4−0] wychodzi mi A' (4,8) a ma być A' (−3,−6) 2. Drugi przypadek robię tak samo tylko, że z literką B zamiast A.(i też jest źle) co robię nie tak? pomocy

mambaxD:

mambaxD:

mambaxD:

Rzeka: Błąd w odpowiedziach.. S(a,b) A'(x',y') A(x,y) k=2 (to ta liczba nad J) [x'−a, y'−b] = k * [x−a, y−b] x'−(−2) = 2*[2−(−2)] y'−(−1) = 2*[4−(−1)] <uklad równań> x'=8−2 y'=10−1 x'=6 y'=9

księżniczka: Rzeka źle napisałaś... przecież, masz tam napisane, że środkiem jednokładności jest punt O a nie S... więc wyjdzie [4, 8]

Mila: Dany jest odcinek o końcach A(2,4) i B(4,−2) oraz punkty O(0,0) i S(−2,−1). a) J²_O k=2 i punkt =(0,0) jest środkiem jednokładności ⇔J²_O(A(2,4))=A'=(2*2,2*4)=(4,8) J²_O(B(4,−2))=B'=(2*4,2*(−2))=(8,−4) b) S=(−2,1) k=2 Jaka ma być skala nie napisałeś To zrobimy wektorowo w drugim wątku.

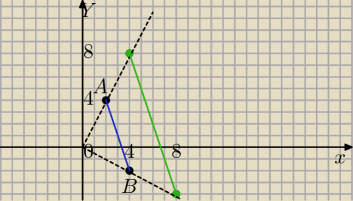
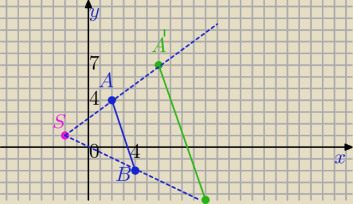
Mila: Dany jest odcinek o końcach A(2,4) i B(4,−2) b)S=(−2,1), k=2 SA^→=[2−(−2),4−1]=[4,3] SA'^→=2*[4,3]=[8,6] S=(−2,1)→[8,6]→A'=(−2+8,1+6)=(6,7) SB^→[4+2,−2−1]=[6,−3] SB'^→=2*[6,−3]=[12,−6] S=(−2,1)→[12,−6]→B'=(−2+12,1+(−6)]=(10,−5) II sposób: Można też liczyć wg wzoru S(a,b) i skala k x'=k(x−a)+a y'=k(y−b)+b A(2,4) i B(4,−2),S=(−2,1) wsp. A' obliczamy tak: x'=2*(2+2)+(−2)=6, y'=2*(4−1)+1=7, A'=(6,7) wsp. B' x'=2(4+2)+(−2)=12−2=10, y'=2*(−2−1)+1=−5, B'=(10,−5)