ułóż równanie kwadratowe donek: Ułóż równanie kwadratowe którego pierwiastkami są podane liczby: x1=¹_4−2√3 oraz x2=¹_4+2√3 nie chodzi bynajmniej o postać iloczynową bo nad tym już myślałem ps: jaka jest komenda na robienie indeksu dolnego? nie znalazłem w tej tabelce z komendami...

donek: oczywiście chodzi o skorzystanie z wzorów Viete'a ale niewiele one wnoszą moim zdaniem...

h3h: postac iloczynowa i pomnoz

master1201: jest nieskonczenie wiele rozwiazan

donek: ale nie znam wspolczynnika a...

master1201: I niestety nie da sie go obliczyc z tych danych

donek: jak to nieskonczenie wiele?

indeks: dolny indeks jest opisany obok

master1201: funkcja moze byc skierowana ramionami w dol i do gory to juz masz 2 wierzcholek funkcji nalezy do zbioru R \ {0}

donek: ^−b_a=2 ^c_a=^−3+2√3₄₈ korzystając z wzorow Viete'a obliczylem tyle. a co dalej? to musi miec rozwiazanie.

donek: a=48 b=−96 c=−3+2√3 48x²−96x−3+2√3 a moze to byc tak?

delta: 4x² − 8x + 1 = 0

master1201: Da sie to rozwiacac ale jest tych rozwiazan nieskonczenie wiele

Eta: ax² +bx =c=0 , a ≠0 x² +^b_ax + ^c_a=0

	1		4+2√3
x1=		=		= 1 +12√3
	4−2√3		16−12

x₂= ............. = 1 −¹₂√3

	−b		b
x1+x2=		= 2 =>		= −2
	a		a

	c
x1*x2=		= 1 −34= 14
	a

zatem: równanie ma postać x²−2x +¹₄=0

master1201: Prosciej wyobraz sobie funkcej o miejscach zerowych 1 i 3 wierzcholek ma wspolrzedne (2, x) ten x to kazda liczba oprocz 0

h3h: x²−√3x−0,25

Eta: oczywiście, równoważne do podanego prze ze mnie ma postać 4x²−8x +1=0

master1201: Eta dlaczego a jest dodatnie a nie ujemne ?

donek: @Eta patrząc teraz wydaje się to banalne ale faktycznie wpadłeś/aś na rewelacyjny pomysł na rozwiązanie tego dzięki bardzo, analogicznie spróbuję zrobić resztę przykładów.

master1201: Wroce do przykladu co podalem wczesniej miejsca zerowe 1 i 3 wierzcholek 2,x x= 0,00001 bardzo plaski wykres x = 100 wykres bardzo wysoki oba spelniaja warunki zadania a maja 2 rozne wzory wiec liczenie takiego zadania poprostu mija sie z celem latwiej napisac ze ma nieskonczenie wiele rozwiazan i to uzasadnic

Eta: z założenia: a≠0 , to wystarczy by podzielić równanie przez "a" i mamy wzory Viete^'a

donek: ale właśnie pierwiastki czyli x₁ i x₂ są miejscami zerowymi więc nie możesz przyjąć sobie dowolnych

master1201: Zgadzam się jest to jedno z przykładowych rozwiązań jednak podkreślam jest ich nieskończenie wiele

Eta: no to ja już podałam 2 równania równoważne daję nastepne: 8x²− 16x +1=0 16x² − 32x +2=0 ¹₂x²− x +¹₈=0 ale wszystkie są równoważne ! zatem wystarczyło podać jedno z nich

delta:

1		4 + 2√3		√3
	=		= 1 +
4 − 2√3		4		2

1		4 − 2√3		√3
	=		= 1 −
4 + 2√3		4		2

	√3		√3		√3		√3		1
(x − (1+		))*(x − (1−		)) = x2 − (1−		)x − (1+		)x +
	2		2		2		2		4

	√3		√3		1		1
= x2 − (1 −		+ 1 +		)x +		= x2 − 2x +
	2		2		4		4

Wszystkie inne rozwiązania mają wielokrotności współczynników tego rozwiązania

Eta:

master1201: Eh nie bede sie klocil poczytajcie o funkcji kwadratowej bo majac 2 miejsca zerowe mozna napisac nieskonczenie wiele wzorow funkcji i nie beda rownowazne. Niektore moga miec a <0 a niektore a>0 wiec nie ma szans zeby byly rownowazne !

master1201: delta w swoich obliczeniach przyjales a =1 a czemu nie a= 1/3 lub a= −2 ?

Eta: master .......... proponuję Tobie to "dokształcenie " Za parę dni napisz ...... co Ci z tego dokształcenia wyszło Powodzenia.

Eta: dla a = −2 mamy równanie: −2x² +4x −¹₂=0 podziel to równanie przez ( −2) otrzymasz równanie równowazne do pierwszego, które podałam na wstepie: x² −2x +¹₄=0

sushi_ gg6397228: niestety MASTER ma racje, przez dwa punkty przechodzi nieskonczenie wiele krzywych drugiego stopnia TYLKO PROSTA PRZECHODZI JEDNA PRZEZ DWA PUNKTY y=a(x−x₁)(x−x₂)

sushi_ gg6397228: jezeli chodzi o rownanie a(x−x₁)(x−x₂)=0 to "a'" nie wpływa na wielosc rozwiazan

think: ale w treści jest że ma ułożyć równanie kwadratowe... nigdzie nie pisze, że ma to być jednoznaczne rozwiązanie, czyli a(x − x₁)(x−x₂) wybiera dowolne a i ma równanie

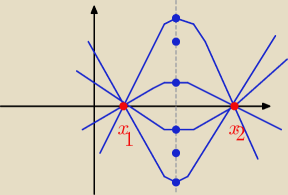
Eta: Parabole są różne ale równania ax²+bx+c =0 gdy dane są ich: x₁, x₂ są równoważne, bo mają te same rozwiązania

Eta: sushi Co to znaczy: " Master ma rację" ........ skoro jej nie ma Master kwestionował : że równania są równoważne Wypadałoby wyprostować, to co teraz Ty napisałeś, bo inaczej to utwierdzasz błędne rozumowanie Mastera

sushi_ gg6397228: Master pisał " nieskonczenie wiele wzorów funkcji" to mialem na mysli y=a(x−x₁)(x−x₂)

think: eee tam nudzicie się tylko i szukacie sobie tematów do zaczepki

Eta: W treści zadania wyraźne było polecenie: wskaż równanie, a nie funkcję więc dlatego wszystkie równania , których pierwiastkami są x₁ i x₂ są równoważne i to wszystko w tym temacie

Eta: i dla think

think: Etunia dobrej nocy i do następnej

Eta: K o l o r o w y c h

Bogdan: Dzień dobry. Polecenie w zadaniu jest jednoznaczne − "ułóż równanie", a nie ułóż wzór funkcji względnie wzór paraboli. Rozpatrzmy problem na następującym prostym przykładzie.

	1
Czym różnią się równania: x − 2 = 0, 2x − 4 = 0,		x − 1 = 0, 235x − 470 = 0, ...?
	2

Czy jest to jedno równanie, czy są to różne równania i jest ich wówczas nieskończenie wiele?