 cześć, chciałabym tylko, żeby ktoś sprawdził czy mam dobry tok rozumowania
ZAD. Wyznacz przedziały monotoniczności i ekstrema funkcji f(x)=ln(1−x2)
roz.
(ln(1−x2))'= (lnu)' *(1−x2)' = 1/(1−x2) * −2x =
= −2x/(1−x2)
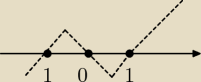
−2x/(1−x2) = 0 dla x=−1, x=0, x=1
czyli:
f. rosnąca dla x∊(−1,0) i (1,∞)
f. malejąca dla x∊(−∞,−1) i (0,1)
maksimum lokalne dla x=0
minimum lokalne dla x =−1 i x=1
z góry dzięki
cześć, chciałabym tylko, żeby ktoś sprawdził czy mam dobry tok rozumowania
ZAD. Wyznacz przedziały monotoniczności i ekstrema funkcji f(x)=ln(1−x2)
roz.
(ln(1−x2))'= (lnu)' *(1−x2)' = 1/(1−x2) * −2x =
= −2x/(1−x2)
−2x/(1−x2) = 0 dla x=−1, x=0, x=1
czyli:
f. rosnąca dla x∊(−1,0) i (1,∞)
f. malejąca dla x∊(−∞,−1) i (0,1)
maksimum lokalne dla x=0
minimum lokalne dla x =−1 i x=1
z góry dzięki
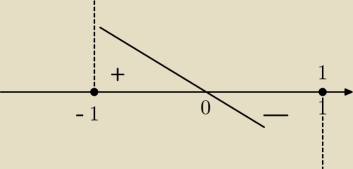 D 1 − x2 > 0 ⇒ x2 < 1 ⇒ x ∊ (−1,1)
D 1 − x2 > 0 ⇒ x2 < 1 ⇒ x ∊ (−1,1)
| 1 | 2x | |||
f'(x) = (In(1 − x2))' = | * (−2x) = − | |||
| 1 − x2 | 1 − x2 |
| 2x | ||
− | = 0 ⇔ −2x = 0 ⇒ x = 0 | |
| 1 − x2 |
| 2x | ||
− | > 0 ⇔ 2x < 0 ⇒ x < 0 | |
| 1 − x2 |

 w sumie myślałam, że będzie gorzej
jeszcze raz dzięki
w sumie myślałam, że będzie gorzej
jeszcze raz dzięki