Proszę o szybką pomoc(ciąg geometryczny) Xiaton: Sporządź wykresy ciągów i określ ich monotoniczność: 1) a_n = 4 * (¹₂)ⁿ⁻¹ 2) b_n = (¹₃) * 2ⁿ⁻¹ 3) c_n = 3 * 1ⁿ⁻¹

Xiaton: pomoże ktoś?

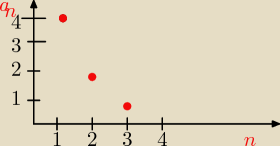
TOmek: 1) a₁=4 a₂=2

	1
a3=4*		=1
	4

Xiaton: dzięki, pomógłbyś mi z resztą zadań, bo narobiłem sobie w szkole spore zaległości i teraz nic z tego nie rozumiem

Xiaton: Wytłumaczyłby mi ktoś jak do tego dojść(na podst 1 zad)?

Xiaton:

Baykowsky: w celu narysowania wykresu podstawiasz sobie za n kilka pierwszych liczb naturalnych. a dla ustalenia monotonicznosci (czy jest rosnacy malejacy czy staly) musisz porownac n−ty wyraz z (n+1)−wszym wyrazem np w zadaniu drugim

	1
bn =		* 2n−1
	3

	1
bn+1 =		* 2n
	3

b_n+1 = 2 * b_n oraz wszystkie wyrazy ciagu sa dodatnie stad b_n+1 > b_n wiec ciag rosnacy

Xiaton: i tak nie kumam, bo dzisiaj po chorobie przyszedłem do szkoły i te ciągi widzę po raz pierwszy, ale dzięki za starania

Baykowsky: sluchaj masz zapisane b z indeksem n. to znaczy ze np 5−ty wyraz ciagu b zachowuje sie tak jak jest to napisane z tym ze za kazdy n musisz wstawic 5. a monotonicznosc to po prostu ustalenie czy kazdy nastepny wyraz ciagu jest wiekszy czy mniejszy od poprzednika

Xiaton: wykresy zrozumiałem, a co do motoniczności, to można przecież odczytać ją z wykresu, no nie?

Godzio: teoretycznie tak a lepiej jest wykazać, bo nigdy nie wiadomo czy przypadkiem nie będzie jakiegoś skoku a_{n + 1} − a_n > 0 −− rosnący a_{n + 1} − a_n < 0 −− malejący b_{n + 1} − b_n = 0 −− stały

Baykowsky: no mozna ale w ten sposob masz udowodniona monotonicznosc i jestes pewien ze nie okaze sie ze np od pierwszego do dwunastego wyrazu ciag jest rosnacy a potem ni z tego ni z owego zaczyna malec

Xiaton: Wielkie dzięki, wreszcie to umiem!