Malutkie zadanko typu "wykaż, że..." jarek.w: Witam. Dostałem takie zadanie, kto może proszę o pomoc: Wykaż, że jeżeli Δ ≥ 0 to funkcja kwadratowa ma dwa pierwiastki (msc. zerowe). Prosiłbym o wytłumaczenie tego dość łopatologicznie bo mam naprawdę solidne problemy z tego typu zadaniami. Z góry dziękuję.

jarek.w: To było moje trzecie zadanie umieszczone na tym forum i po raz trzeci ANI JEDNEJ odpowiedzi... dzięki, a w tej stronie pokładałem wszystkie pozostałe mi nadzieje.

think: jeżeli Δ ≥ 0 to oznacza, że istnieje √Δ 1^o Δ > 0

	−b + √Δ		−b − √Δ
wtedy mamy dwa pierwiastki x1 =		oraz x2 =
	2a		2a

funkcja przyjmuje postać a(x − x₁)(x − x₂) 2^o Δ = 0

	−b
wtedy jest jeden pierwiastek podwójny x0 =
	2a

wtedy funkcja przyjmuje postać a(x − x₀)² = a(x − x₀)(x − x₀) czyli dla Δ ≥ 0 mamy dwa pierwiastki

think: nie dramatyzuj chłopie, po prostu to jest takie zadanie że właściwie nie wiadomo co trzeba zrobić aby ktoś był usatysfakcjonowany, gdybyś wrzucił coś normalnego do policzenia, pewnie zwaliłoby się kilku chętnych

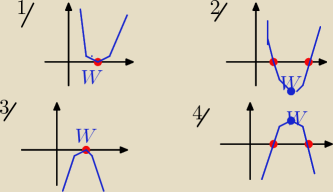
Eta: 2 sposób: W( x_w, y_w) => W( −^b_2a , ^−Δ_4a) 1/ a>0 y_w=0 −−− jedno miejsce zerowe zatem:

	−Δ
		=0 => Δ=0
	4a

podobnie dla 3/

	−Δ
dla 2/ yw<0 i a >0 =>		<0 => −Δ<0 => Δ>0 −−− dwa różne miejsca zerowe
	4a

	−Δ
podobnie dla 4/ a <0 i yw >0 =>		>0 => Δ >0 −−− dwa różne miejsca zerowe
	4a

wniosek: f(x) = ax²+bx +c dla a≠0 i Δ≥0 −−− ma dwa miejsca zerowe

jarek.w: poprostu jeżeli naprawdę tutaj nie zasięgnę porady to nie mam kogo się złapać. a odnośnie zadania... no dzięki.

think: proszę

think: ale na przyszłość trzymaj się jednej ksywy, bo wtedy pomagający widzą, że ktoś wrzuca zadania a nie otrzymuje odpowiedzi bo sprawdziłam na forum i jako jarek.w wrzuciłeś tylko to zadanko.

jarek.w: masz rację ale właśnie myślałem że w taki sposób otrzymam "drugą szansę". nie chce spamować forum

think: wystarczy w zadaniu wpisać: " podbijam" czasami jest tu wrzucane tyle zadań na raz, że po prostu to jedno wśród nich się gubi i koniec końców zostaje nie zrobione