Jak zbadać liczbę rozwązań równania z parametrem m czad__: Zad.1 Zbadaj liczbę rozwiązań równania w zależności od wartości parametru m: x²−6|x|+8=m Zad.2 Dla jakich wartości parametru m równanie |x²−4|=m²+1 ma dwa różne rozwiązania. Bardzo proszę o rozwiązanie tych dwóch zadań, bo nie mam pojęcia jak je zrobić ; ((

Godzio: umiesz narysować chociaż te wykresy ?

czad__: Mam właśnie problem z narysowaniem tych wykresów.... Ja myślałem, że trzeba rozpocząć to od narysowania wykresów dla x>0 i x<0, wtedy wychodzą mi 4 miejsca zerowe, ale nie wiem co dalej ; ((

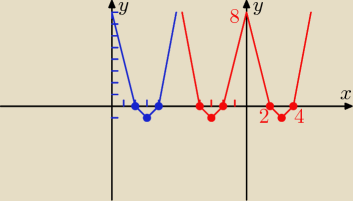
Godzio: Zad 1. Najpierw rysuje wykres: f(x) = x² − 6x + 8 Następnie korzystam z symetrii częściowej względem OY ( f(|x|) ) f(x) = |x|² − 6|x| + 8 = x² − 6|x| + 8 − a tak prosto to wymazuję lewą stronę wykresu i odbijam to co jest po prawej na lewą No to lecimy: f(x) = x² − 6x + 8 = (x − 4)(x − 2) = (x − 3)² − 1 −− to możesz sobie wszystko wyliczyć x₁ = 4, x₂ = 2, p = 3, q = −1 i teraz: dla m ∊ (−∞, −1) −−− 0 rozwiązań dla m ∊ (8, ∞)∪{−1} −−− 2 rozwiązania dla m ∊ (−1,8) −−− 3 rozwiązania Analogicznie 2: Rysujesz wykres f(x) = x² − 4 Nakładając bezwzględność |f(x)| korzystamy z symetrii częściowej względem OY , prostymi słowami: to co jest na dole odbijamy na górę, i tak powstaje f(x) = |x² − 4| jak sobie nie poradzisz to już pomogę ale chociaż spróbuj

czad__: z pierwszym przykładem poradziłem sobie− dziękuję za pomoc ,z kolei w tym drugim mam wykres, ale nie wiem jak mam dalej zrobić z tym : m²+1, żeby miało dwa różne rozwiązania

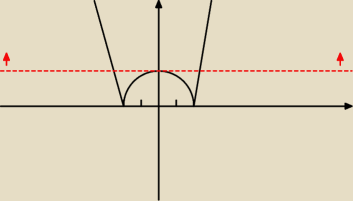
Godzio: dla m² + 1 ∊ (4, ∞) mamy 2 rozwiązania czyli musisz rozwiązać nierówność: m² + 1 > 4 −−− i to da Ci rozwiązanie, wracając do tamtego 4 rozwiązania oczywiście a nie 3 i dodatkowo dla m = 8 są 3 rozwiązania

czad__: Dzięki bardzo, w końcu zrobiłem to drugie zadanie ; D