| sin2x − |sinx| | ||
f(x)= | x∊(0,π)∪(π, 2π). Narysuj wykres i wyznacz miejsca zerowe. | |
| sinx |

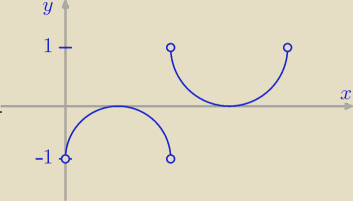 D: sinx ≠ 0 ⇒ x ≠ kπ
1o Dla x ∊ (0, π) ⇒ sinx > 0 ⇒ |sinx| = sinx
D: sinx ≠ 0 ⇒ x ≠ kπ
1o Dla x ∊ (0, π) ⇒ sinx > 0 ⇒ |sinx| = sinx
| sin2x − sinx | ||
f(x) = | = sinx − 1 | |
| sinx |
| sin2x + sinx | ||
f(x) = | = sinx + 1 | |
| sinx |
| π | 3 | |||
Miejsca zerowe: x = | i x = | π | ||
| 2 | 2 |