zadanie z parametrem Lu: dla jakich wartości parametru m równanie (m−1)x²−2mx+m−2=0 ma dwa różne pierwiastki rzeczywiste. mój problem polega na tym, że nie wiem jak mam zaznaczyć wszystko na osi i jak dojść do końcowego rozwiązania

Svanar: Δ > 0 m−1 ≠ 0 → m ≠ 1 tylko podstawić

Godzio: ma dwa różne pierwiastki rzeczywiste: Δ > 0 , i żeby w ogóle były te pierwiastki to a ≠ 0 ⇒ m − 1 ≠ 0 ⇒ m ≠ 1 Policz deltę i oblicz m dla jakiego jest > 0

Kejt: a=m−1 b=−2m c=m−2 równanie kwadratowe ma dwa rozwiązania wtedy i tylko wtedy gdy: Δ>0 Δ=b²−4ac więc musi być: b²−4ac>0 podstaw i licz.

Kejt: no tak + oczywiście założenia, o których zawsze muszę zapomnieć..

Svanar: ^^

Lu:

	2
z delty wychodzi 12m−8 i jak podstawie i oblicze do końca to m >
	3

Godzio: no i dobra wywalasz 1 z rozw. i koniec

Lu: a jakby było, że równanie ma 2 różne pierwiastki dodatnie?

Godzio: do tego co wyżej dodajesz założenia:

	−b
x1 + x2 > 0 ⇒		> 0
	a

	c
x1 * x2 > 0 ⇒		> 0
	a

TOmek: http://rfeter.republika.pl/matematyka/parametr/parametr.html pozdrawiam

Lu: i jak dojść do wyniku? bo o założeniach wiem, wiem ile z nich wyjdzie, ale nie wiem jak mogłabym przedstawić to graficznie na osi,żeby dojść do całkowitego rozwiązania

Godzio: Podaj rozwiązania z każdego założenia to Ci to rozrysuje

Lu: x₁ + x₂ m₁=0 m₂=2 x₁ * x₂ m₁=1 m₂=2

	2
Δ>0 m>
	3

ale nie jestem pewna czy napewno dobrze obliczyłam

Godzio: Dobra to w takim razie sprawdzę, przy okazji dostaniesz pełne rozwiązanie bo nie chce mi się na kartce sprawdzać

Lu: dziękuje

Godzio: (m−1)x²−2mx+m−2=0 a ≠ 0 ⇒ m ≠ 1 Δ > 0 ⇒ Δ = 4m² − 4(m² − 3m + 3) = 12m − 12 > 0 ⇒ m > 1 −−− czyli tu się walnąłeś

	2m
x1 + x2 > 0 ⇒		> 0 ⇒ m(m − 1) > 0 ⇒ m ∊ (−∞,0) ∪ (1,∞)
	m − 1

	m − 2
x1 * x2 > 0 ⇒		> 0 ⇒ (m − 2)(m − 1) ⇒ m ∊(−∞,1) ∪ (2,∞)
	m − 1

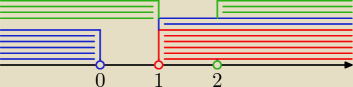
Część wspólna jak widać: m ∊ (2,∞)

Maciek: Godziu poza samym liczenie to Ty ladnie rysujesz

Lu: dzieki

Godzio: Sie nabrało wprawy