Równanie i nierówność kwadratowa z parametrem oswiecony: 1) Dla jakiej wartosci parametru m rownanie x²−2(m−2)x−4m=0 ma 2 rozwiazania ujemne? 2) Dla jakich wartosci p. m zbiorem rozwiazan nierownosci (5−m)x²−2(1−m)x+2(1−m)<0 jest zbior wszystkich liczb rzeczywistych? Prosze o rozwiazania...

sushi_ gg6397228: kiedy beda dwa rozwiazania

think: ad 1 skorzystaj ze wzorów viete'a 2 rozwiązania ujemne gdy: Δ > 0 x₁*x₂ > 0 x₁ + x₂ < 0

oswiecony: no tak, czaje, ale prosilbym o wyrachowanie tych zadan

think: nie złociutki, umiesz liczyć... licz na siebie, czyli rachuj sam, możesz tutaj to zawsze ktoś sprawdzi czy dobrze, ale my za Ciebie tego nie policzymy.

oswiecony: uwierz, probowalem... szczegolnie tej nierownosci nie czaje − nie wiem jak sie zabrac... Jakby ktos rozrysowal, to moze bym zrozumial

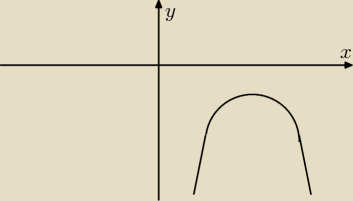
Godzio: Żeby nierówność była zawsze prawdziwa cała parabola musi być pod wykresem więc muszą być spełnione warunki: a < 0 −−− ramiona są do dołu, Δ < 0 −−− nie ma pierwiastków

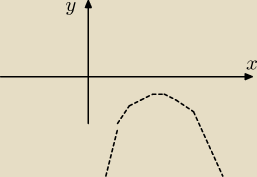
think: dopasuj warunki jakie muszą spełniać a, Δ, x₁, x₂ i co tam jeszcze się da aby w tym drugim otrzymać taką postać funkcji kwadratowej jak na rysunku.

oswiecony: to juz wiem, ale co do 1) to warunki mialem, nie potrafie poprostu policzyc

think: odpowiedz na takie pytania: 1) kiedy funkcja kwadratowa ma dwa pierwiastki? 2) kiedy są one ujemne

oswiecony: a z tej strony nie moze byc?

think: może akurat nie ma żadnego znaczenia, bo na to z której strony będzie nie ma warunków

oswiecony: 1) delta wieksza od 0 2) kiedy ich suma jest ujemna i iloczyn dodatni

Godzio: może, to były rysunki pokazowe

think: najważniejsze aby było nad, lub pod osią x−ów lub się z nią stykało tudzież ją przecinało

think: dobrze, to policz Δ i sprawdź dla jakich m jest ona > 0

oswiecony: czyli dla tej nierownosci sa 2 warunki 1) Δ<0 2) a<0 tak?

think: później skorzystaj ze wzorów Viete'a

	c
x1*x2 =
	a

	b
x1 + x2 = −
	a

think: tak

think: ehh i dlatego w jednym poście umieszcza się jedno zadanie, bo później są problemy jak przeplatają się podpowiedzi do różnych zadań...

oswiecony: czyli nie mam co liczyc na rachunek zadania? Swoich wypocin wstydze sie wypisywac...

think: nie wstydź się my też się mylimy dawaj jak się skompromitujesz obiecuję, że usunę

oswiecony: wole nie, na lekcji dosc sie nacierpialem... ale juz chyba wiem

think: oswiecony, nikt tutaj nie będzie się nabijał ani robił złośliwości, jeśli nie chcesz mieć właśnie takich przykrości na lekcji to rób i rób jak najwięcej dawaj!

oswiecony: x²−2(m−2)x−4m=0 1) Δ>0 Δ=(4−2m)²−4*1*(−4m) Δ=16−16m+4m²+16m Δ=4m²+16 4m²+16>0 4m²>−16 m²>−4 m>−2 lub m<2 2) x₁*x₂>0 x₁=2m x₂=−4 −8m>0 m<0 3) x₁+x₂<0 2m−4<0 2m<4 m<2 m∊(−∞;2) teraz mozesz skrytykowac...

think: 4m² + 16 jest zawsze większe od 0 bo m² jest liczbą nieujemną także nie ma rozwiązania coś takiego, że m² = −4 bo nie ma pierwiastka kwadratowego z liczby ujemnej, w każdym razie w liczbach rzeczywistych. kumasz?

think: także z warunku Δ > 0 wyszło Ci, że to akurat jest dla każdego m prawdziwe.

oswiecony: no tak, to logiczne, ale nie wiem jak to zawrzec w zadaniu btw. sa liczby inne niz rzeczywiste?

think:

	c		−4m
ad 2) x1*x2 =		=
	a		1

źle podstawiłeś

think: są jeszcze liczby zespolone

think: jak nie wiesz jak skorzystaj z warunków dla funkcji kwadratowej a>0 i Δ < 0 czyli przyjmuje tylko wartości dodatnie zauważ, że w 4m² + 16 4 > 0 i Δ = 0² − 4*4*16 = −256 < 0

oswiecony: dzieki wielkie za pomoc, a najbardziej za motywacje, biore sie zaraz za ta nierownosc liczby zespolone... to chyba nie moje sfery

think: spoko jak tutaj spędzisz więcej czasu może nie będzie Ci się to wydawało takie kosmiczne dzięki, że się nie poddałeś

oswiecony: tak dla formalnosci 1) parametr m∊(−∞;0) tak?

think: tak

think: a masz odpowiedzi do tych zadań? bo nie przymierzając, zadania z parametrem to takie w których najprościej się machnąć

oswiecony: no wlasnie nie mam, ja spadam, dobranoc dzieki za wszystko

think: dobrej nocy

TOmek: x²−2(m−2)x−4m=0 Δ=(−2(m−2))²−4*(−4m)*1 hmm

TOmek: juz wiem...