pole trojkata julka09: dane sa wierzcholki trojkata a=2;−1 b=4;2 c 5;1 wyznacz pole trojkata abc i rownanie prostej zawierajacej wysokosc trojkata poprowadzona z wierzcholka a

think: 1) policz długość odcinka bc 2) wyznacz prostą przechodzącą przez punkty B, C 3) policz odległość punktu A od prostej BC 4) później wyznacz prostopadła do prostej BC przechodzącą przez A (to będzie równanie prostej zawierającej wysokość trójkąta)

	1
5) co do pola P =		*|BC|*{odległość punktu A od prostej BC}
	2

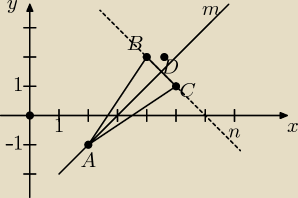
think: prosta n: wyznacz wzór prostej przechodzącej przez punkty BC prosta m: prosta prostopadła do n przechodząca przez punkt A |AD| długość odcinka AD to jest wysokość trójkąta ABC, liczysz ją ze wzoru na odległość punktu A od prostej n.

	1
P =		|AD|*|BC|
	2

wzór na długość odcinka A = (x_a, y_a) B = (x_b, y_b) |AB| = √(x_a − x_b)² + (y_a − Y_b)² wzór na odległość punktu P = (x_p, y_p) od prostej L: Ax + By + C = 0

	|Axp + Byp + c|
odległość P od L =
	√A2 + B2

julka09: dziękuje

think: mam nadzieję, że teraz jesteś w stanie zrobić to zadania

Gustlik: Think, pole trójkąta łatwiej liczy się z wyznacznika wektorów: Z dwóch boków trójkąta "robimy" wektory w ten sposób, żeby miały poczatek w jednym punkcie, np. AB^→ i AC^→ A=(2;−1) B=(4; 2) C=(5; 1) Liczymy współrzędne tych wektorów wg zasady "współrzedne końca" − "współrzędne początku": AB^→=B−A=[4−2; 2−(−1)]=[2; 3] AC^→=C−A=[5−2; 1−(−1)]=[3; 2] Liczymy wyznacznik tych wektorów: d(AB^→; AC^→) = |2 3| ← współrzędne wektora AB^→ |3 2| = ← współrzędne wektora AC^→ =2*2−3*3= (na krzyż: pierwsza przekątna − druga przekatna) =4−9=−13 Pole trójkąta liczymy ze wzoru:

	1		1		13
P=		|d(AB→; AC→)|=		*|−13|=		=6,5
	2		2		2

Odp: P=6,5.