wielomian z parametrem wojtek_90: dany jest Wielomian W(x) = x⁴ − (m−2)x² +m ; wyznacz parametr m dla których wielomian ma: a) 2 pierwiastki b) 0 pierwiastków c) 1 pierwiastek d) 3 pierwiastki e) 4 pierwiastki

Mickej: Zaczynasz od podstawienia pod x²=t oczywiście z tego wynika że t≥0 a dalej to już uzależniasz od Δ z tym że to będą rozwiązania dla parametru t i będziesz je jeszcze musiał spierwiastkować względem x więc dla x będzie 2 razy więcej rozwiązań zawsze

Mickej: A bez wzorów vieta się nie obejdziesz

Mickej: nie psuć mu zabawy niech sam robi ewentualnie podpowiadać ale nie rozwiązujcie przynajmniej od razu

wojtek_90: dzięki za odp. ale nadal nie wiem jak mam znaleśc 3 i 1 pierwiastek prosilbym o pomoc

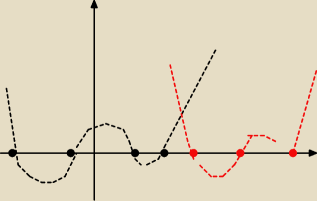
think: odpowiednio przesuwając wykres zawsze można otrzymać liczbę pierwiastków ∊ {0,1,2,3,4} w każdym razie dla x⁴ czerwoną linią pokazany przykładowy z 3 rozwiązaniami, sam pokombinuj jak to ma być

Mickej: niesamowite te wykresy ale jeżeli troszkę pomyślisz to sam stwierdzisz że to jest niemożliwe

wojtek_90: jeśli to nie możliwe to może powie ktoś wprost jak to rozwiazać zależy mi natym bo mam jeszcze pare podobnych zadań i na tym przykladzie chcialbym się czegoś nauczyć a narazie to mam mentlik w głowie

Godzio: W(x) = x⁴ − (m − 2)x² + m x² = t , t ≥ 0 t² − (m − 2)t + m 4 rozwiązania: Δ > 0 , t₁ * t₂ > 0 , t₁ + t₂ > 0 2 rozwiązania, Δ > 0, t₁ * t₂ < 0 0 rozwiązań Δ < 0 Nie mam pojęcia jak zrobić z 1 lub 3 rozwiązaniami

think: t² − (m − 2)t + m = 0 1^o Δ > 0 ⇒ t₁,t₂ i jeśli t₁ i t₂ są dodatnie do mamy 4 rozwiązania jeśli t₁*t₂ ujemne to mamy 2 rozwiązania jeśli t₁*t₂ = 0 to mamy 1 rozwiązanie jeśli t₁*t₂ >0 i t₁ + t₂ < 0 to wtedy jest 0 rozwiązań 2^o Δ = 0 ⇒ mamy t₀ jeśli t₀ > 0 to mamy dwa rozwiązania jeśli t₀ = 0 to mamy jedno rozwiązanie jeśli t₀ < 0 brak rozwiązań 3^o najfajniejszy Δ < 0 nie ma rozwiązań.

Bogdan: Podaję komplet założeń. ax⁴ + bx² + c = 0. 0 rozwiązań dla: * Δ < 0

	b
* Δ = 0 i −		< 0
	a

	b		c
* Δ > 0 i −		< 0 i		> 0
	a		a

1 rozwiązanie dla: * b = 0 i c = 0

	b
* Δ > 0 i −		< 0 i c = 0
	a

	b
2 rozwiązania dla: * Δ = 0 i −		< 0
	a

	c
*		< 0
	a

	b
3 rozwiązania dla: * −		> 0 i c = 0
	a

	b		c
4 rozwiązania dla: * Δ > 0 i −		> 0 i		> 0
	a		a

Jak widać, równanie nie ma rozwiązań również dla przypadku Δ = 0 oraz dla Δ > 0

wojtek_90: serdeczne dzięki za podpowidź w zadaniu