Cześć!
Jak mogę wyznaczyć odcinek łączący ramiona dowolnego trapezu równoległy do podstaw tak, by
podzielił trapez na dwa mniejsze o równych polach?
Porównałam pola dwóch trapezów:
P1=P2
0,5h1*(a+b)=0,5 h2*(b+c)
h1*(a+b)=h2*(b+c)
Co dalej?
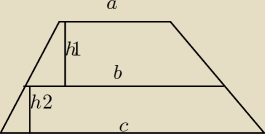
Oj Godzio. Twój zapis nie odnosi się do tego rysunku, bo podstawy na rysunku Niki
zostały oznaczone literkami: c, a − to po pierwsze. Po drugie − średnią geometryczną długości
podstaw trapezu ma odcinek dzielący trapez nie na dwa trapezy o równych polach, a na
dwa trapezy podobne.
Odcinek EF o długości c dzieli trapez ABCD na dwa trapezy: ABFE i EFCD o równych polach.
|AB| = a, |CD| = b, |EF| = c
ha − wysokość trapezu ABFE, hb − wysokość trapezu EFCD.
| a + c | b + c | |||
Z równości trapezów ABFE i EFCD: | * ha = | * hb | ||
| 2 | 2 |
| ha | b + c | |||
Stąd | = | |||
| hb | a + c |
| ha + hb | a − b | ha | a − b | ||||
= | ⇒ | + 1 = | |||||
| hb | c − b | hb | c − b |
| b + c | a − b | ||
+ 1 = | |||
| a + c | c − b |
| a2 + b2 | ||
Z ostatniej równości otrzymujemy c2 = | ⇒ c = √ (a2 + b2) / 2 | |
| 2 |
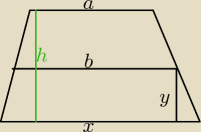
mam jeszcze pytanie jeżeli chcę rozwiązać to układem równań:
{1/2(a+x)*(h−y) = 1/2(b+x)*y
{1/2(a+x)*(h−y) = 1/2(a+b)*h
to też wyjdzie mi na końcu √(a2+b2)/2 czy może inny wynik
Może mi ktoś jeszcze wytłumaczyć to przejście
| b+c | a−b | ||
+1= | |||
| a+c | c−b |
| a2+b2 | ||
c2= | ||
| 2 |
| b + c | a − b | |||
Przekształć sama równość | + 1 = | tak, aby otrzymać c. | ||
| a + c | c − b |
