Pole trapezu ce es: Korzystając z twierdzenia Ptolemeusza oblicz pole trapezu prostokątnego wpisanego w okrąg, w którym odcinki poprowadzone ze środka okręgu do końców dłuższej podstawy maja długości 8√2 oraz 17

Kejt: znasz to twierdzenie? ;>

ce es: znam

Kejt: jestem tylko ciekawa jakim cudem oni chcą wpisać trapez prostokątny w okrąg.. chyba, że to taka podpucha, bo z tego prostokąt wychodzi ;>

Godzio: Co prawda to prawda pewnie chodziło o trapezu opisanego na okręgu prawda ce es ?

Kejt: Twierdzenie Ptolemeusza. W czworokącie wpisanym w okrąg iloczyn długości jego przekątnych jest równy sumie długości iloczynów długości boków przeciwległych

Kejt: chyba, że były dwa, to zwracam honor

ce es: chodzilo mi o trapez opisany, zwracam honor

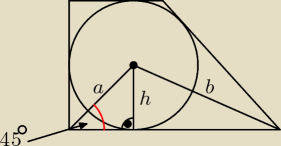
Kejt: b=17 a=8√2 a=h√2 chyba nie będzie dalej problemu? ;>

ce es: Ja wiem jak rozwiązać to zadanie tylko to jest zadanie odemnie

Kejt: to weź uprzedzaj paskudo jedna

ce es: Powodzenia życzę

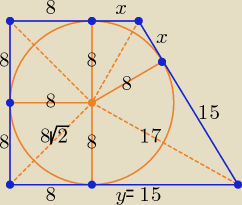
Bogdan: Twierdzenie Ptolemeusza mówi, że w dowolnym czworokącie wpisanym w okrąg iloczyn długości przekątnych równa się sumie iloczynów długości boków przeciwległych. Jeśli trapez jest opisany na okręgu, to twierdzenie Ptolemeusza nie ma zastosowania. Sytuację przedstawia rysunek, podaje potrzebne obliczenia bez wyjaśnień, mam nadzieję, że są zrozumiałe. y = √17² − 8² = 15

x		8		64
	=		⇒ x =
8		15		15

Bogdan: ce es czy takie rozwiązanie miałeś na myśli?

ce es: Tak

tim: Witaj Bogdan, jakby ktoś zatęsknił za Timem, to wróciłem ! Nie wiem na jak długo, ale zobaczymy.

Bogdan: No nareszcie timie pojawiłeś się , witaj. W której szkole jesteś?

tim: Wiadomo Tą co wymarzyłem 3 LO w Gdyni. Wakacje były, początek szkoły, nie było oakzji i czasu.

Kejt: w gdyni? och, to u mnie

tim: Tak? Łał. Miło poznać

Bogdan: Tak myślałem, że wybierzesz szkołę z międzynarodową maturą. Podoba Ci się ta szkoła?

tim: Bogdanie, jeżeli znajdziesz moment, to na maila starego [matura@vp.pl] wysłałem prośbę. Jeżeli znajdziesz czas i chęć to rozpatrz, a jak nie to nie . Nie rób sobie problemu. A więc wróciłem na posterunek... Z kolejnymi tysiącami zadań, które są identyczne co roku... Ah.

Kejt: trójka.. podziwiam.

tim: Ale międzynarodowej matury nie zamierzam pisać. Na razie − po trzech tygodniach − mogę stwierdzić, że tak. Atmosfera świetna, uczniowie z każdym da się dogadać, nauczyciele wymagający, ale to liceum .

tim: A ty Kejt, gdzie?

Kejt: w plastyku skończyłam. Nie wiem co ja tam robię, no ale pisząc maturę rozszerzoną z matematyki i fizyki pewnie przejdę do historii szkoły

tim: Oooo. Znam tam parę osób . Łooo hooo... No to ciekawie .

Bogdan: Właśnie timie przeczytałem Twojego maila. Przyjrzę się temu.

tim: Dobrze, nie rób sobie problemu .

Kejt: bardzo. nauczycielka od matematyki ma mnie już dosyć..heh.

tim: Nie dziwie się, plastyk + rozszerzona matematyka i fizyka = zdziwienie. A znasz jakieś pierwszaki?

Kejt: kogoś tam znam.. a o kogo konkretnie chodzi?

tim: Alicję, taka mała blondynka..

Kejt: bardzo mała? i troszkę przy sobie? chyba okulary nosi..

tim: Okularki z pomarańczowymi oprawkami, jest na fotografii Kojarzysz?

Kejt: chyba wiem która..

tim: No to mamy nawet wspólnych 'znajomych' . Ok. Moje gadu: 5556527, to jakby co .