Trygonomeria!!! Parkerx: Zad1. Dla jakich X∊( −π/2 ; π/2) liczby tgx ;1 ; cosx/1+sinx są w podanej kolejności trzema początkowymi wyrazami malejącego ciągu arytmetycznego (an)? Zad2. Sporządź wykres funkcji: f(x)=sin2x*tgx Zad3. Dla jakich wartości parametru a układ sinx*siny= 1/4 cosx*cosy=a (spięte klamrą) ma rozwiązanie? Zad4. Wyznacz te liczby rzeczywiste x które spełniają układ 1/4^x +1 = 5/2^x+1 ( 4 jest do potegi x a 2 do potegi x+1 ) sinx*cosx≥ 0.25 Prosze o pomoc w rozwiązaniu zadań. Z góry dziękuję.

Godzio: zał. 1 − sinx ≠ 0 sinx ≠ 1

	π
x ≠
	2

	cosx
2 * 1 = tgx +
	1 + sinx

	sinx		cosx
2 =		+
	cosx		1 + sinx

	sinx + sin2x + cos2x
2 =
	(1 + sinx)cosx

	1 + sinx
2 =
	(1+sinx)cosx

	1
2 =
	cosx

	1
cosx =
	2

	π		π
x = −		v x =		− ustal dla jakiego x jest to ciąg malejący
	3		3

zad2. cosx ≠ 0

	π
x ≠		+ kπ
	2

	sinx
f(x) = 2sinxcosx *		= 2sin2x −− z tym chyba sobie już poradzisz
	cosx

zad 3.

	1
sinx * siny =
	4

cosx * cosy = a / * −−−−−−−−−−−−−−−−−−−−−−−−−

	1
sinxcosx * sinycosy =		a
	4

2sinxcosx * 2sinycosy = a sin2x * sin2y = a −−−− maksymalne przedziały to: −1 ≤ sin2x * sin2y ≤ 1 a ∊ <−1,1> zad . 4

	1		5
(		)x + 1 =		+ 1 −−− tak to wygląda ?
	4		2x

sinxcosx ≥ 0,25

Parkerx: do zadania 4. nie w liczniku jest 1 a w mianowniku 4 do potęgi x i dalej +1(jako wolny wyraz) = 5 podzielić przez 2 do potęgi (x+1)

Parkerx: a tak wogule to mam pytanie co do wykresy funcji 2sin²X pomijajac 2 z przodu czyli patrzac na sin²x bedzie to wygladało tak ze wartosci ujemne sinx trzeba odbić przes oś Y

Godzio: 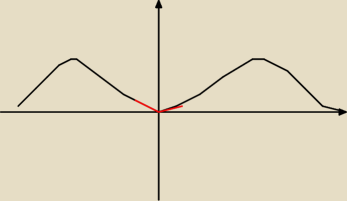w ogóle To jeszcze się upewnię:

1		5
	+1 =
4x		2x+1

gdyby odbić to byś miał funkcję |sinx| a tutaj tak lekko przechodzi

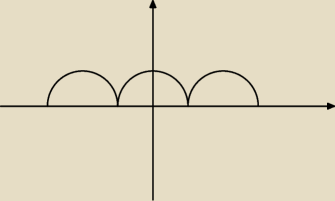
Godzio: To jest |sinx|

Parkerx: do zad4. tak teraz napisałeś dokładnie tak jak w przykładzie i do tego część wspólna z sinxcosx≥0,25

Godzio:

1		5
	+ 1 =
4x		2x + 1

2^−2x + 1 = 5 * 2^{−x − 1} 2^−x = t

	5
t2 + 1 =		t
	2

2t² − 5t + 2 = 0 Δ = 25 − 16 = 9

	5 + 3
t1 =		= 2
	4

	5 − 3		1
t2 =		=
	4		2

2^−x = 2 ⇒ x = − 1

	1
2−x =		⇒ x = 1
	2

sinxcosx ≥ 0,25 / * 2

	1
2sinxcosx ≥
	2

	1
sin2x ≥
	2

	π		5π
2x =		+ 2kπ v 2x =		+ 2kπ
	6		6

	π		5π
x =		+ kπ v x =		+ kπ
	12		12

	π		5π
x ∊ (		+ kπ,		+ kπ)
	12		12

Nie wiem jak to się ma do tego wyżej hmmm

Bogdan: Zad.3. Niech a∊<−1, 1>

	1
sinx siny =
	4

cosx cosy = 1 + −−−−−−−−−−−−−−−

	1
cosx cosy + sinx siny = 1
	4

	1
cos(x − y) = 1		sprzeczność bo cos(x − y) ∊ <−1, 1>
	4

a więc a∉<−1, 1>

Hania: Godzio na wykresie masz wartość bezwzględną z coś x, a nie sinx.

Hania: Dodatkowo do założeń w zad. 1 nie sinx−1 różne od zera, tylko sinx+1 różne od zera. To może wpływać znaczo co na dziedzinę funkcji.

Jerzy: Rację masz,ale to są już kopaliny z przed paru lat. Co to znaczy „znaczo co” ?