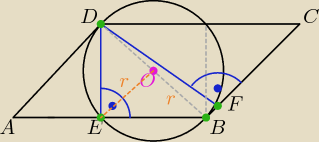
 ZADANIE: Boki równoległoboku mają długości 6 cm i 10 cm, a kąt ostry ma miarę 60 stopni. Z
jednego wierzchołka kąta rozwartego poprowadzono dwie wysokości. Oblicz obwód czworokąta
wyznaczonego przez spodki tych wysokości i przez wierzchołki kątów rozwartych. Wyznacz długość
promienia okręgu opisanego na powstałym czworokącie.
DANE:
|kąt DAE| = 60 stopni.
|kąt ADC| = 120 stopni.
SZUKANE:
r = ?
ZADANIE: Boki równoległoboku mają długości 6 cm i 10 cm, a kąt ostry ma miarę 60 stopni. Z
jednego wierzchołka kąta rozwartego poprowadzono dwie wysokości. Oblicz obwód czworokąta
wyznaczonego przez spodki tych wysokości i przez wierzchołki kątów rozwartych. Wyznacz długość
promienia okręgu opisanego na powstałym czworokącie.
DANE:
|kąt DAE| = 60 stopni.
|kąt ADC| = 120 stopni.
SZUKANE:
r = ?
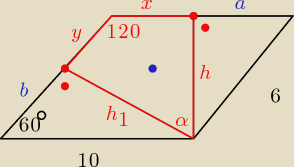
| h1 | ||
sin60o = | ||
| 10 |
| h | ||
sin60 = | ||
| 6 |
| b | ||
cos60 = | ||
| 10 |
| a | ||
cos60 = | ||
| 6 |
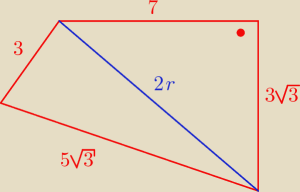 Ok, to kończąc:
4r2 = 72 + (3√3)2
4r2 = 76
r2 = 19
r = √19
Ok, to kończąc:
4r2 = 72 + (3√3)2
4r2 = 76
r2 = 19
r = √19

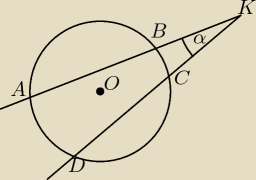 Wykaż, że miara kąta α między dwiema siecznymi przecinającymi się w punkcie K równa się połowie
różnicy miar kątów środkowych odpowiadających łukom AD i BC zawartym między tymi siecznymi.
Wykaż, że miara kąta α między dwiema siecznymi przecinającymi się w punkcie K równa się połowie
różnicy miar kątów środkowych odpowiadających łukom AD i BC zawartym między tymi siecznymi.



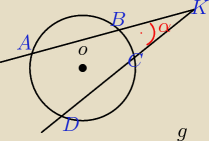 Wykaż:
| ∡α|=1/2 (|∡AOD|− |∡BOC|)
Wykaż:
| ∡α|=1/2 (|∡AOD|− |∡BOC|)