Geometria-kłopoty;D Kamil: Nie wiem kompletnie jak zabrać się do tego zadania, nie musicie robić po prostu pomóżcie powiedzcie jak itp. albo stronkę gdzie wytłumaczone bo znaleźć nie moge pamiętam, że robiłem takie kiedyś ale nie pamiętam jak : W trójkąt równoramienny ABC w którym |AB| = 24 i |BC| = |AC|=20, wpisujemy prostokąt tak, że bok tego prostokąta zawiera się w boku AB, a pozostałe wierzchołki należą do ramion. Podaj wymiary prostokąta o polu największym

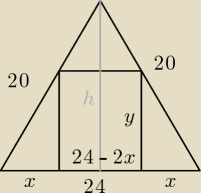Godzio: Obliczam wysokość: h² + 12² = 20² h = 16 Z podobieństwa wyliczam y:

h		y
	=
12		x

4
	x = y
3

	4		8
P▭ = y * (24 − 2x) =		x(24 − 2x) = −		x2 + 32x
	3		3

wierzchołek x_w paraboli − dla niego pole osiąga największą wartość:

	8		3
xw = U{−32}{2 * (−		) = 32 *		= 6
	3		16

	4		4
y =		x =		*6 = 8
	3		3

Wymiary prostokąta o największym polu: 8 x 6

Kamil: hhmm a jakoś prościej? bo nieogarniam trochę tego jak wyliczyłeś xw

Godzio: można jakoś też tak: Jeśli pole prostokąta ma być największe to suma 3 pól trójkątów jest najmniejsza

Kamil: jak ten wierzchołek wyliczyłeś

Godzio:

	−b
ze wzoru: f(x) = ax2 + bx + c wierzchołek p =
	2a

Kamil: właśnie się zorientowałem dzieki wielki jeszcze raz