różne ala: Spróbuję podsumować swoje wczorajsze "wypociny".Możecie sprawdzić,skorygować,wytłumaczyć? Podaj liczbę rozwiązań rzeczywistych równania 15−7x⁴=0 −7x⁴+15=0 (x²−√¹⁵₇)(x²+√¹⁵₇)=0 (x−⁴√¹⁵₇)(x+⁴√¹⁵₇)(x²+⁴√¹⁵₇) x₁=⁴√¹⁵₇,czyli mamy jedno rozwiązanie... Podaj dziedzinę funkcji f(x)=√12−3x−√3−x 12−3x≥0 x≤4 3−x≥0 x≤3 x∊(−∞,3> Rozłóż na czynniki wielomian W(x)=x⁴−16 W=(x²+4)(x−2)(x+2) Wskaż liczbę ,która nie jest liczbą całkowitą: a)log2√2{3}+log26 b)log_√22 c)log₂60−log 215 d)log₂√2 a,b.c=2,więc pozostaje odp d .Podaj zbiór wartości funkcji f(x)=IxI+2 tego nadal nie rozumiem..

Svanar: |x| ≥0 dla dowlonego R wiec |x| + 2 ≥ 2 dla dowolnego R wiec ZW = <2, +∞)

sushi_ gg6397228: a rysunek umiesz zrobic, wczoraj go nawet "wypocilem" wiec podstawiaj po kolei liczby calkowite, zacznij od −10 i podstawiaj kolejno pod "x" −9,−8,−7,..., 5 , 6, ,7 ,8, 9,10 co zauwazysz

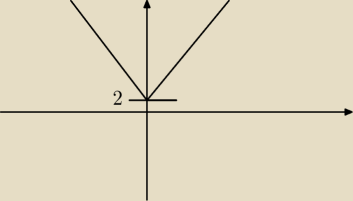
Svanar: rysunek mniej−wiecej taki.... poszukaj na necie, będą duuuuuużo dokładniejsze

ala: Dziękuję bardzo,a pozostałe zadania dobrze?

Svanar: ostatnie dobrze, wielomian tez, dziedzina tez a w pierwszym zgubiłaś jedno rozwiązanie: −⁴√¹⁵₇

ala: Aaaa,no tak...dzięki bardzo