Pomóżci mi bo sama nie dam rady:(
Beti: Nie potrafię rozwiązać nierówności:
| | 1 | | 1 | |
a) |
| − |
| −1<0 |
| | log2x | | log2x−1 | |
21 wrz 22:35
MM: no to jad kobry.
21 wrz 22:39
Beti: Czekam...pomóżcie mi − mam trzy przykłady, które nie potrafię rozwiązać:(
21 wrz 22:41
sushi_ gg6397228: dziedzina, wspolny mianownik
21 wrz 22:42
sushi_ gg6397228:
| 1 | | 1 | |
| − |
| −1<0 |
| log2 x | | log2 {x−1} | |
czy
| 1 | | 1 | |
| − |
| −1 <0 |
| log2 x | | log2 (x) −1 | |
21 wrz 22:46
Beti: pierwsza wersja
21 wrz 22:48
Beti: Czy Df.: x∊(0; +
∞)


21 wrz 22:53
sushi_ gg6397228:
jezeli by byla druga wersja, to sie robi podstawienie i jest po sprawie
co do pierwszej wersji to praktycznie jest niewykonalne, wiec zobacz jeszcze raz
21 wrz 22:53
sushi_ gg6397228: dziedzina x−1>0 i x>0 czyli x>1
21 wrz 22:54
Beti: w zbiorze jest dokładnie tak jak napisałam w poleceniu
21 wrz 22:55
sushi_ gg6397228: rysunek to nie byl moj, Ktos spamuje,
zrob zdjecie tego zadania ze zbioru, bo jezeli to ma byc podstawa to optuje za 2 wersja
21 wrz 22:59
sushi_ gg6397228: jezeli nie ma nawiasu to jest (log2 x) − 1 a wtedy robi sie przez podstawienie
21 wrz 23:01
sushi_ gg6397228: | 1 | | 1 | |
| − |
| − 1<0 i dalej jak prosty wielomian |
| t | | t−1 | |
21 wrz 23:02
Beti: nie nie... jest dokładnie tak jak napisałam w poleceniu
21 wrz 23:02
Beti: aha no właśnie tak...ale dalej mi wyszło, że t∊(0;1) czy to jest dobrze

?bo za t podstawiłam
log
2x
21 wrz 23:05
sushi_ gg6397228:
wiec mowie, ze takiej wersji nie policzysz log2 (x−1) bo tylko komputer moze zrobic rysunek,
wiec twierdze ze bedzie log2 x − 1
21 wrz 23:05
Beti: aha...też nad tym zastanawiałam się ale ok przyjmiemy twoją wersję
21 wrz 23:08
sushi_ gg6397228:
tak 0<t<1 i powrocic po pierwotnego podstawienia
0<log2 x <1
0<log2 x <log2 2
x<2 i dziedzina x>0 czyli x∊(0,2)
21 wrz 23:09
sushi_ gg6397228: w ksiazce by dali nawiasy, aby nie bylo watpliwosci

21 wrz 23:10
Beti: no właśnie ale ich nie ma...
ale dziedzina funkcji to x>1 a nie x>0, a poza ytym w odpowiedziach w książce jest napisane że
x∊(0,1)∪(2, +∞)
21 wrz 23:14
sushi_ gg6397228: nic z tych rzeczy mamy log2 x wiec mamy x>0
21 wrz 23:18
sushi_ gg6397228:
mnozysz przez (−1) wiec sie zienaiznak nierownosc
t>1 lub t<0
21 wrz 23:20
Beti: aha no tak tak....
21 wrz 23:21
sushi_ gg6397228:
wspolny mianownik daje
(t
2+t−1)*t(t−1) >0
t(t−1)>0
21 wrz 23:22
Beti: sushi, jeśli możesz rozpisz mi to bo się zapętliłam

21 wrz 23:22
sushi_ gg6397228:
0=log2 1 ==> x<1
1= log2 2 ==> x>2
i dziedzina x>0
21 wrz 23:23
sushi_ gg6397228:
robimy wspolny mianownik i dostajemy to co napisalem wczesnij
t(t−1)>0
t<0 lub t>1
log2 x <0 lub log2 x >1
log2 x < log2 1 lub log2 x >log2 2
x < 1 lub x > 2 oraz dziedzina x>0 ==> x∊(0,1) ∪ (2; +∞)
21 wrz 23:27
Beti: sushi, z moich obliczeń wynika, że t2−7+1 dzielone na (t2−t)>0
21 wrz 23:27
sushi_ gg6397228: zapisz wszystkie obliczenia, mi wychodzi w lcizniku
−t2+t−1 −−−> delta ujemna wiec tylko t(t−1)>0 bierze sie pod uwage
21 wrz 23:31
Beti: tak wzięłam i wyszło mi, że t∊(−∞;0)∪(1;+∞)
21 wrz 23:33
sushi_ gg6397228: wyszlo t
czyli t<0 lub t>1
podstawiamy teraz za "t" ==> "log2 x
21 wrz 23:36
sushi_ gg6397228: co tam masz wiecej do zrobienia, bo powoli czas do spania sie zbliza

21 wrz 23:47
Beti: jest...otrzymałam właściwy wynik − wielkie dzięki sushi

mam jeszcze jedno, chyba trudniejsze

:
| | 3 | |
0,26− |
| > 3√0,0082log</sup>4</sup>x−1 |
| | log4x | |
21 wrz 23:51
Beti: pomyliłam się zaraz podam właściwy przykład
21 wrz 23:52
Beti: tam za 0,008 jest w wykładniku 2log4x−1 a z lewej strony nierówności ten ułamek jest w
wykładniku
21 wrz 23:53
Beti: sushi mam nadzieję, że jeszcze nie poszedłeś spać...

21 wrz 23:57
sushi_ gg6397228: 
21 wrz 23:59
sushi_ gg6397228: 3√0.008= 0,2
22 wrz 00:00
sushi_ gg6397228:
podstawa mniejsza od 1 wiec zajmujemy sie wykladnikiem i ZMIANA ZNAKU NIEROWNOSCI
22 wrz 00:00
sushi_ gg6397228:
| | 3 | |
6− |
| < 2 log4 x − 1 |
| | log4 x | |
22 wrz 00:01
sushi_ gg6397228:
robimy porzadki; podstawienie t= log4 x ;na jedna strone; wspolny mianownik
22 wrz 00:06
sushi_ gg6397228:
ile tam wyliczylas t

22 wrz 00:11
Beti: wyszło t∊(−∞;1/2)∪(3;+∞) tzn. t<−1/2 ; t>3
22 wrz 00:12
sushi_ gg6397228:
zapomnialas o t=0 z mianownika, wiec po poprawce bedzie ....
22 wrz 00:13
Beti: czyli t>3 tak

22 wrz 00:15
sushi_ gg6397228: sa trzy miejsca zerowe , fala zrobiona

dwa z licznika i jeden z mianownika, ktory cichaczem wedruje do licznika
22 wrz 00:17
Beti: sushi, wyszło mi x=64 ale co dalej to nie wiem − chyba już za późno na myślenie logiczne

22 wrz 00:18
sushi_ gg6397228:
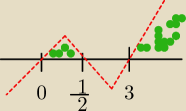
22 wrz 00:20
22 wrz 00:21
sushi_ gg6397228:
x∊(1; 2) ∪ (64; +
∞)

a na dobranoc poprosze kołysankę

22 wrz 00:27
Beti: sushi, bardzo ci dziękuję za pomoc, ale ja już odpływam − poddaję się, niestety jest już zbyt
późno, za 5 godzin muszę wstawać. Jeszcze raz wielkie dzięki

22 wrz 00:31
Beti: hi hi hi

22 wrz 00:33


 ?bo za t podstawiłam
log2x
?bo za t podstawiłam
log2x



 mam jeszcze jedno, chyba trudniejsze
mam jeszcze jedno, chyba trudniejsze :
:




 dwa z licznika i jeden z mianownika, ktory cichaczem wedruje do licznika
dwa z licznika i jeden z mianownika, ktory cichaczem wedruje do licznika


 a na dobranoc poprosze kołysankę
a na dobranoc poprosze kołysankę 

