Pytanie Godzio: Mam 2 pytania Jeśli masz daną funkcję kwadratową z parametrem i polecenie to znaleźć ten parametr żeby był spełniony warunke: |x₁| + |x₂| ≤ 1 1 pytanie czy założeniem będzie Δ > 0 2 czy mogę sobie obustronnie podnieść do kwadratu czy osobno rozpatrywać przypadki ? x₁² + 2|x₁x₂| + x₂² ≤ 1

niedouczony: polecenie brzmi dwa pierwiastki, czy dwa różne pierwiastki?

bibi: jeśli chodzi o 1 to wg mnei oki 2. rozpisałbym następująco: |x₁| + |x₂| ≥ |x₁ + x₂|, czyli |x₁ + x₂| ≤ |x₁| + |x₂| ≤1

Godzio: ... dla których pierwiastki trójmianu ...

Godzio: bibi myślałem o tym tylko co mi to da ?

Jack: Wg mnie oba są ok. Pewnie zadanie jest na wzory Viete'a więc chodzi o dwa różne pierwiastki. Tego się domyślam bo nie znam treści, ale na to wygląda.

Kamil: Godzio obiecałeś sie zapytać o książki z matmy pamiętasz

Godzio: Dobra to w takim razie będzie trzeba rozpatrywać przypadki dla m, dzięki

Eta: Śmiało podnosimy do kwadratu ..... bo obydwie strony nierówności są dodatnie

Godzio: Kamilu mówiłem żebyś to Ty o to zapytał bo wieczorem jest więcej kompetentnych ludzi ja tera idę swoje zadania robić

Kamil: a napiszesz mi jakies zadanie z logarytmu prosze

bibi: z mojego wzoru masz prostą obustronną nierówność i korzystając z Viete'a otrzymujesz wprost rozwiązanie 2−ego warunku

Godzio: Eta zastanawiałem się nad tym bo znalazłem coś takiego: https://matematykaszkolna.pl/forum/50080.html i już nie byłem pewny

Kamil: a z logarytmu coś dostane Godzio prosze?

Kamil: chodzi mi zadanie na podstawowa matematyke Godzio plis?

Kamil: Godzio podasz zadanie z logarytmu prosze

Kamil: Prosze

Kamil: chce poczwiczyć logarytmy a nie mam nowych przykładów Godzio prosze

Kamil: napiszesz mi Godzio w nowym poscie jak napisze prosze

Kamil: napisze w nowym poscie prosze Godzio podasz mi napisz

Godzio: ehhh Kamil ... wpisz w googlach hasło "logarytmy przykłady" to na pewno coś Ci wyskoczy

Kamil: Ty masz wiele książek pewnie Godzio

czekolada: hahahah : ) Kamil daj mu spokój on też coś musi zrobić dla siebie ; ) google nie gryzie! Znajdziesz tak jak Godzio napisał dużo przykładów i zadań wraz z odpowiedziami.

Kamil: ale na podstawową

Kamil: a ktos może mi powiedzic ksiązka do matematyki do matury Kiełbasa jest dobra

Godzio:

	7		1
A(		,		)
	2		2

	4 + √3		1
B(		,		)
	2		2

	4 − √3		1
C(		,		)
	2		2

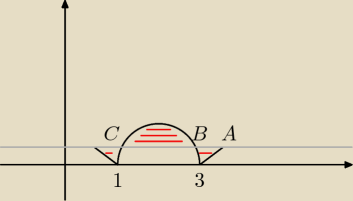
f(x) − to są te linie 2 g(x) − półokrąg czy jeśli mam policzyć pole tego obszaru to dobrze robię ? :

	1		1
P = | 2 * ∫7/23(f(x) −		) + ∫3(4+√3)/2(g(x) −		) +
	2		2

	1
∫(4+√3)/2(4−√3)/2 (		− g(x) ) |
	2

Godzio: pobijam

Jack: tę kopułę tak: ∫cx bx (g(x) −1/2) dx

Godzio: Ok dzięki

Jack: kawałeczki tak: (prawy) ∫bx 3 (1/2 −g(x))dx +∫ 3 ax (1/2 −f(x) )dx A że lewy jest taki sam, to to wszystko razy 2.

Godzio: No dobra czyli wszystko namotałem Dzięki jeszcze raz

Jack: spoko, i tak robisz zadania ponad−licealne wiec masz prawo...

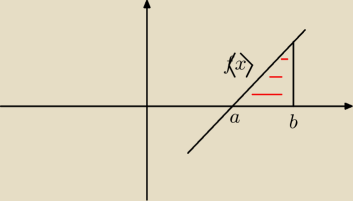
Godzio: Czyli tak ogólnie, całka z tego pola to będzie: ∫^a_b(f(x) − 0 )dx = ∫^a_bf(x)dx ?

Godzio: zawsze się mylę w tych przedziałach

Jack: Ja się z kolei mylę przy graniach całkowania (to przez to, że inaczej zapis wygląda w zeszycie, inaczej tu na forum)... wszędzie tam, gdzie zapisałem te granice powinno być odwrotnie. Większa wartość x powinna być nad całką, mniejsza pod całką. Teraz zauważyłem bo zrobiłeś tak, jak ja wcześniej. Poza tym równość jest prawdziwa.

Godzio: Czyli to co napisałem na początku jest poprawne ?

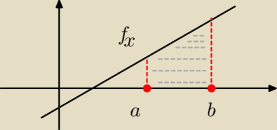
Jack: Tak, ale dobry nawyk to tak zapisywać całkę: P_pole=∫^b_a ( f(x)−0) dx. (Pierwszy zapis) Ty zapisałeś P_pole=∫^a_b (0−f(x) ) dx Jest to poprawne bo ∫^a_b f(x) dx = −∫^b_a f(x) dx oraz a*∫ f(x) dx = ∫a*f(x) dx Ale ideę oddaje lepiej ten pierwszy zapis.

Jack: (jeśli cokolwiek Ci to mówi, jest to zgodne z ideą całki w sensie Riemanna)

Godzio: Dobra, wbije se to do głowy