lukas: Rozwiąż nierówność: 4x²+1<0 a=4, b=0, c=1 Δ=0−16=−16 parabola nie ma miejsc zerowych wiec x∊R może ktoś to sprawdzić bo nie wiem czy to rozumiem

Student: to że nie ma miejsc zerowych nie oznacza że x∊R tylko że akurat w tym przypadku nierówność jest niespełniona

lukas: to jak będzie w tym przypadku?

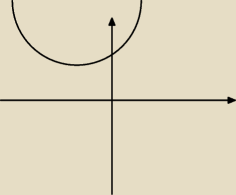
TOmek: 4x²+1<0 nie ma zadnej liczby która po wstawieniu po "x" da warunek liczby "mniejszej od zera" sprawdzmy 4*1²+1<0 sprzecz. 4*(−8)²+1<0 sprzecz z resztą 4x²+1<0 Δ=0−16 Δ=−16 −> brak miejsc zerowych funckja ma a=4 czyli jest dodatnie (ramiona skierowane do góry a jest warunek 4x²+1<0 także na moje brak rozwiązania. Ja tak myśle, niech ktoś z górnej półki(Eta,think,Godzio,Bogdan, itp) to udowodni

lukas: Dziękuje bardzo już rozumiem.

Jack: Jesli szukamy x∊R (a zwykle tak szukamy) to wychodzi zbiór pusty. 4x²+1<0 x²<−¹₄ −−−− nie istnieje liczba R która podniesiona do kwadratu jest mniejsza od 0. Rys. trochę koślawy bo niepotrzebnie przesunięty z osi OY w lewą stronę (ale że w górę to prawidłowo).

TOmek: dziekuje za nie docenienie mojego talentu malarskiego xd

Jack:

Bogdan: Zadanie. Rozwiązać nierówność 4x² + 1 < 0. Rozwiązanie. ∀_x∊R 4x² + 1 > 0, więc rozwiązaniem nierówności jest x∊∅ Zapis ∀_x∊R czytamy: dla każdej wartości x∊R albo dla dowolnej wartości x∊R. Znak ∀ nazywamy kwantyfikatorem ogólnym albo kwantyfikatorem dużym.

fds: 6ΩΔδγα≥∫∫⇔⇔≈