pole obszaru ograniczonego wykresami funkcji marta: oblicz pole obszaru ograniczonego wykresami funkcji y= 2 + x − 2x² − x³, y= 0

bartuś: chętnie pomógłbym Ci ale nie potrafię...

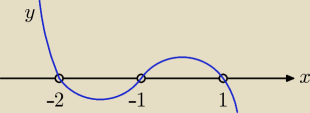
Bogdan: Narysuj ten wykres. Czy w zadaniu są podane jeszcze inne linie ograniczające obszar, którego pole należy wyznaczyć? Trzeba tu zastosować całkę oznaczoną.

marta: tylko to jest podane, a jak mam narysować wykres?

Bogdan: Wyznacz miejsca zerowe funkcji.

Bogdan: −x³ − 2x² + x + 2 = −x²(x + 2) + (x + 2) = −(x + 2)(x − 1)(x + 1) Jeśli chodzi tu o obszary zawarte między miejscami zerowymi i osią x, to pole P jest równe: −1 1 ∫ (−y) dx + ∫ y dx −2 −1

marta: punkty 1, −1, −2

marta: dziękuję

Marta: Ja mam ogromny problem z rozwiązaniem poniższego zadania: Oblicz pole obszaru ograniczonego funkcjami: f(x) = x² −1 g(x)= x−1 Proszę bardzo o pomoc!

Marta: I jeszcze jedno zadanko niestety. Przedziały monotoniczności i ekstrema f(x) 2x⁴+4x²+1 Proszę o pomoc, z góry dzięki !

Mila: Oblicz pole obszaru ograniczonego funkcjami: f(x) = x² −1 g(x)= x−1 x²−1=x−1 x²−x=0 x(x−1)=0 x=0 lub x=1 granice całkowania od 0 do 1. ₀∫¹(x−1−(x²−1))dx=₀∫¹(−x²+x)dx