Narysuj wykres MMM: Narysuj wykres y= x− [ x ]

Kejt: czy to ma być wartość bezwzględna? [x]

Tomek.Noah: o ile sie nie myle to jest cecha

Kejt: hmm.. czyli lepiej żebym tego nie ruszała..

sushi_ gg6397228: to pewnie jest calosc z liczby [x]

Tomek.Noah: no tak to jest "najlbizsza wartosc calkowita liczby np [−1,1]=1 [0,2]=0 itp

MMM: chodzi o cechę

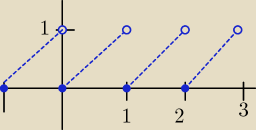
sushi_ gg6397228: calosc to po prostu obcianie ulamka od liczby calkowitej pokazuje kawalek wzoru funkcji , reszta rysunku bedzie analogiczna

	⎧	x−1 dla 1≤x<2
f(x)=	⎨	x−2 dla 2≤x<3
	⎩	x−3 dla 3≤x<4

sushi_ gg6397228:

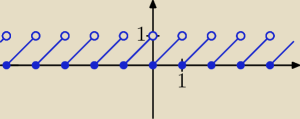
Bogdan: Funkcja f(x) = x − [x] wyznacza część ułamkową argumentu. Rysunek przedstawia jej wykres.

sushi_ gg6397228: odcinki maja kat 45 stopni nachylenia do osi OX

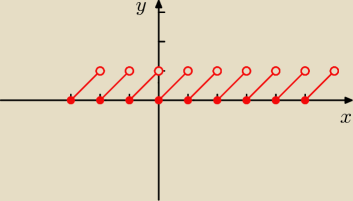
Godzio: [x] −− jest to największa liczba całkowita nie większa od x

	1
np. [		] = 0
	2

	1
[1		] = 1 itd.
	4

więc dla każdej liczby całkowitej x wartość x − [x] będzie równa zero

	1
podstawiając inne pkt np. x =
	4

1		1		1		1
	− [		] =		− 0 =
4		4		4		4

	3
x = 2
	4

	3		3
2		− 2 =		−−− zawsze będzie pozostawać ten ułamek
	4		4

MMM: dzięki wszystkim za pomoc