prosze o pomoc marcin: Wszystkie krawędzie ostrosłupa prawidłowego czworokątnego mają długość 6. Oblicz pole powierzchni i objętość ostrosłupa.

sushi_ gg6397228: co to jest za bryła

Adam: już piszę, moment

sushi_ gg6397228: niech Marcin poda odpowiedz, z łatwoscia sam wyliczy PP i V, jak bedzie wiedzial co to za bryła

bibi: P_c = P_b + P_p P_p = a² = 36

	1
Pb = 4 *		ah = 2ah
	2

	1
(		a)2 + h2 = a2
	2

	3
h2 =		a2
	4

	√3
h =		a
	2

h = 3√3 P_b = 2*6*3√3 = 36√3 P_c = 36 + 36√3 = 36(1 + √3)

bibi: H − wysokość ostrosłupa d = a√2 = 6√2

	1
(		d)2 + H2 = a2
	2

	1
H = √a2 −		d2
	4

	1
H = √36 −		*72 = √18 = 3√2
	4

	1
V =		*Pp*H
	3

	1
V =		*36*3√2 = 36√2
	3

Adam: Pole pow. całk = Pp + Pole ścian bocznych Pole podstawy = 6*6=36 Pole ścian bocznych = 4*1/2a*h h−wysokość ściany bocznej a − połowa podstawy = 3 z Twierdzenia Pitagorasa liczymy h 3² + 6² = h² 9 + 36 = h² 45 = h² h= 3√5 pole 1 ściany bocznej = 3*3√5 = 9√5 Pc = 36 + 4 * 9√5 = 36 + 36√5 = 36(1+√5) jednostek² V= Pp * H * 1/3 H−wysokość ostrusłupa trzeba najpierw obliczyć połowę przekątnej podstawy, aby mieć wymiary trójkąta prostokątnego (połowa przekątnej podstawy, wysokość ostrosłupa, krawędź boczna) połowa podstawy = 1/2a√2 = 3√2 Twierdzenie Pitagorasa na H (3√2)²*H²=6² 18*H²=36 H²=2 H=√2 V= 36 * √2 * 1/3 = 12√2 jednostek³

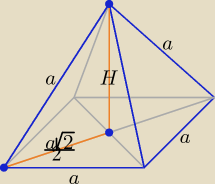
Bogdan: Niepotrzebne jest obliczanie długości h, bo ściany boczne są trójkątami równobocznymi.

	a√2
a = 6, (		)2 = (3√2)2 = 18, H = √ 36 − 18 = √ 18 = 3√2
	2

	1
Pole powierzchni P = a2 + 4 *		a2√3 = 36 + 36√3
	4

	1		1
Objętość V =		*a2*H =		*36*3√2 = 36√2
	3		3