oblicz odległość środka koła wpisanego Monika: w trójkącie równoramiennym ramię o długości 30cm jest nachylone do podstawy pod kątem, którego sinus jest równy 0,6. Oblicz odległość środka koła wpisanego w ten trójkąt od wierzchołków podstawy.

sushi_ gg6397228: zrob rysunek , z sinusa obliczysz H trojkata

Monika: obliczyłam i co dalej?

sushi_ gg6397228: oblicz z Pitagorasa polowe podstawy a potem wzor na pole trojakta

a*H		a+b+c
	=		* r
2		2

z tego wyliczysz "r" SA=H−r

Monika: dzięki wielkie za pomoc pomożesz mi jeszcze z takim zadaniem: w trójkącie prostokątnym cotangens jednego z kątów ostrych jest równy 2. Oblicz stosunek promienia koła opisanego na tym trójkącie do promienia koła wpisanego w ten trójkąt

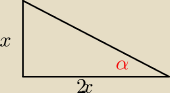
sushi_ gg6397228: wyliczymy z Pitagorasa trzeci bok i prownamy pola

a+b+c
	* r= a*b*c4R
2

a,b,c beda zalezne od "x"

R
	=...
r

Monika: czyli ten trzeci bok będzie równy y=x√5 tak?

sushi_ gg6397228: tak

Monika: a jak mam porównać te pola? bo coś mi chyba nie wychodzi

sushi_ gg6397228: podstawiasz pod "a" b" c" liczby wyjdzie liczba*x*r= ^{liczba* x}_R masz zaleznosc przy okazji R= polowa przeciwprostokarnej (√5x ) wiec wtedy wylicz "r" ze wzoru a*b=(a+b+c)* r

sushi_ gg6397228: a*b= 2x² a+b+c= x+2x+√5x= x(3+√5) 2x²= x(3+√5) * r ===> r= ....

R		0.5 *x* √5
	=
r		co wyjdzie u gory z "r"

Monika:

	3√5 + 5
ostateczny wynik jaki mi wyszedł to
	4

Monika: mam jeszcze takie zadanko w koło wpisano kwadrat, a następnie w ten kwadrat wpisano koło. Wartość bezwzględna różnicy pól tych kół jest równa 8π cm2. Oblicz pole kwadratu

sushi_ gg6397228: rysunek zrobiony

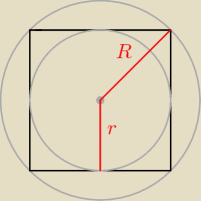
Kejt: a − bok kwadratu d − przekątna kwadratu

	1
R=		d
	2

	1
r=		a
	2

dodatkowo, ze wzoru na przekątną: d=a√2 R²−r²=8π musisz tylko podstawić. w razie czego pytaj.

Kejt: poprawka: πR² −πr²=8π

Monika: dziękuję a pomożesz mi z jeszcze jednym zadaniem?

sushi_ gg6397228: jaka jest tresc zadania

Monika: W trójkąt ostrokątny ABC, w którym |AB|= 8 oraz wysokość |CH| = 6 , wpisano kwadrat DEFG , tak że bok DE jest zawarty w boku AB, a wierzchołki F, G należą do boków AC i BC Oblicz pole tego kwadratu

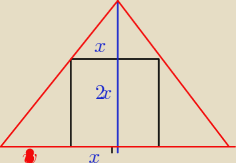
sushi_ gg6397228: w zadaniu moze brakuje ze to trojkat rownoramienny wtedy Tales

6−2x		6
	=
x		4

Monika: x to połowa boku kwadratu?

sushi_ gg6397228: tak, 2x to caly bok to jest zrobione dla trojkata rownobocznego, bo dla dowolnego to krucho to widze

Monika: tylko jakiś dziwny wynik mi wychodzi

sushi_ gg6397228:

	24
2x=
	7

	24
pole= (		)2
	7

Monika: tak zrobiłam

sushi_ gg6397228: inaczej nie da rady, jezeli to nie jest trojkat rownoramienny, bo dla dowolnego to by nie mozna bylo zrobic proporcji

Monika: to teraz już naprawdę ostatnie zadanie w trapezie ABCD w którym AB|| CD i |AB| = 2|CD|, punkt O jest punktem wspólnym przekątnych trapezu.Oblicz stosunek pola trójkąta ABO do pola trapezu

Godzio:

	3a * h
Pt =
	2

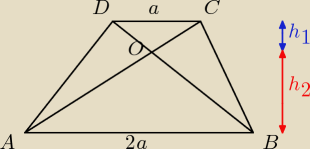
h = h₁ + h₂

h1		a		1
	=		⇒ h1 =		h2
h2		2a		2

h = 1,5h₂

	2a * h2
PAOB =
	2

PAOB		2a * h2		2		2		4
	=		*		=		=
Pt		2		3a * 1,5h2		4,5		9

Monika: bardzo dziękuję za pomoc