Oblicz promień kuli Santos: W kulę wpisano walec o promieniu podstawy 2,5cm i wysokość 12cm.

bibi: r − promień walca R − promień kuli h − wysokość walca (2r)² + h ² = (2R)² 4r² + h² = 4R²/:4

	4r2 + h2
R2 =
	4

	√4r2 + h2
R =
	2

podstaw wartości dane w zadaniui po zabawie

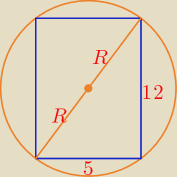Bogdan: Jest okazja do porozmawiania o liczbach nazywanych trójkami Pitagorasa lub trójkami pitagorejskimi. Trójką Pitagorasa nazywamy każdą trójkę (a, b, c) liczb naturalnych takich, że a² + b² = c², np.: 3² + 4² = 5², 5² + 12² = 13², 7² + 24² = 25², 8² + 15² = 17², 9² + 40² = 41², itd. Takich trójek jest nieskończenie wiele. Zaliczamy do nich również wielokrotności pierwotnych trójek, np.: 6² + 8² = 10², 9² + 12² = 15², 10² + 24² = 26², itd. Wszystkie pierwotne trójki Pitagorasa (a, b, c) otrzymujemy z zależności: x = m² – n², y = 2mn, z = m² + n², biorąc za m, n wszystkie pary liczb naturalnych względnie pierwszych, w których jedna z liczb m, n jest parzysta, a druga nieparzysta oraz m > n. Każdą trójkę pierwotną otrzymujemy w ten sposób tylko jeden raz. W zadaniach szkolnych najczęściej wykorzystuje się dwie trójki pitagorejskie: 3, 4, 5 i 5, 12, 13. *********************************************************************************************** W tym zadaniu mamy do czynienia z trójką: 5, 12, 13, 2R = 13 ⇒ R = 6,5. *********************************************************************************************** Tę wiedzę można zastosować np. podczas egzaminu maturalnego przy udzielaniu odpowiedzi w zadaniach zamkniętych.