WYZNACZ WZÓR FUNKCJI KWADRATOWEJ W POSTACI KANONICZNEJ kArOliNa: 1.wyznacz wzór funkcji kwadratowej w postaci kanonicznej wiedząc że wierzchołkiem tej paraboli jest punkt W(−1,3) i do wykresu tej funkcji należy również punkt A(−6,13) 2.wyznacz wzór funkcji kwadratowej w postaci kanonicznej jeśli największa wartością tej funkcji jest liczba zero osią symetrii jej wykresu jest prosta o równaniu x=5 i parabola tej funkcji przecina oś oy w punkcie A(0,−100) POMOŻE MI KTOŚ? BO NIE MAM POJĘCIA JAK DO TYCH ZADAŃ PODEJŚĆ. .

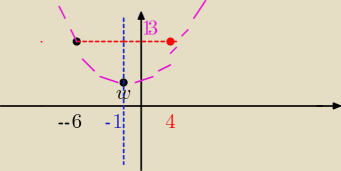
sushi_ gg6397228: W jest wierzcholkiem wiec punkt A jest o 5 jednostek w lewo wiec tez punkt np B musi byc 5 jednostek w prawo i miec taka sama wspolrzedna "y" czyli mamy trzy punkty (−1,3) (−6,13) (4, 13) robimy uklad rownan 3x3 y=ax²+bx+c podstawiamy pod "x" i "y" kolejne punkty

mila: y=ax²+bx+c to jest postac ogólna y=a(x−p)²+q to jest postac kanoniczna wiesz co to jest i jak sie liczy p i q

kArOliNa: szczerze? nadal tego nie czaję bo mnie wtedy na lekcji nie było

sushi_ gg6397228: to moze na przykladzie y=x² (0.0) jest wierzcholkiem A=(2,4) to mamy punkt o 2 jednostki od wierzcholka w prawo , wiec dla punktu o 2 jednostki w lewo (tj x= −2 ) y tez musi dac 4

sushi_ gg6397228: to moze tak zrob uklad wspolrzednych zaznacz W oraz A dokladnie przez W poprowadz prosta prostopadla do osi OX, znajdz punkt symetryczny ( rownoodlegly od prostej) wzgledem punku A

kArOliNa: czyli że jak ? sory ale ciemna jestem z matmy .

kArOliNa: no i potem jak to narysuję to co ?

mila: Wierz jak wyglada parabola ?

kArOliNa: wiem

mila: a wiesz jaki ma wzor jezeli jej wierzchołek jest w srodku układu współrzednych ?

kArOliNa: nom

sushi_ gg6397228:

sushi_ gg6397228: masz 3 punkty to uklad rozwiazujemy y=ax²+bx+c 13=a(−6)²+b(−6)+c 13=a(4)²+b(4)+c 3=a(−)²+b(−)+c

mila: y=x² jezeli jej ramiona są skierowane w górę albo y=−x² jeżeli ramiona sa w dół rysowałaś kiedys parabolę ?

sushi_ gg6397228: 3=a(−1)² +b(−1) +c tak powinno byc w 3−cim rownaniu

kArOliNa: no rysowałam xd no mila to to wiem a po tym rozwiązaniu co mi to daje jak mam wyliczyć to a?

sushi_ gg6397228: masz trzy zmienne a,b,c jak to obliczysz to sobie wyznaczysz postac kanoniczna

mila: chcesz zrozumiec to po kolei bo nie wiem gdzie nie rozumiesz parabola moze być przesunieta w góre lub w dół w lewo lub prawo .I wtedy nie ma już wzoru y=x² ( tu a=1 ) a np y=2x²+5x−5 z tej postaci nie możesz powiedziec gdzie ma wierzchołek

	1
ale jezeli zapiszesz w postaci kanonicznej to tak y=2(x+114]2−8
	8

	1		1
współrzedne wierzchołka to p iq p=−1		q=−8
	4		8

jeżeli masz dany wierzchołek to mozesz znależć postac kanoniczna rozumiesz?

kArOliNa: a czaję i co dalej ?

kArOliNa: czyli że te współrzędne wierzchołka p=−1 i q=3

mila: p to współrzedna wierzchołka x natomiast q to wspłrzedna wierzchołka y czyli twój wierzchołek w(−1,3) ma p=−1 i q=3 znasz wzory na p i q ?

kArOliNa: p= −b/2a q=minus delta/4a

mila: z postaci ogólnej y=ax²+bx +c

	−b		−Δ
p=		q=
	2a		4a

Δ umiesz liczyć ?

mila: ok czyli podstaw za p −1 i wyznacz b

kArOliNa: delta = b² −4ac

kArOliNa: czyli b =2a* (−1)

mila: podstaw tez 3 za q i wyznacz Δ

mila: −b=−2a czyli b=2a

kArOliNa: czyli −Δ= 4a*3

mila: Δ=12a

kArOliNa: i co dalej ?

mila: a teraz napisz wzór na obliczanie Δ i będziesz podstawiała co sie da czyli b=2a i Δ=12a

kArOliNa: czyli 12a=4a²−4ac

sushi_ gg6397228: a nie lepiej podstawic do y=a(x−p)²+q wartosci "p","q" i x=−6, y=13 aby wyliczyc "a"

Bogdan: Proponuję następujące rozwiązanie. W każdym z podanych zadań podany mamy wierzchołek paraboli W = (x_w, y_w) oraz punkt A do niej należący. Zastosujemy mając te dane postać kanoniczną: y = a(x − x_w)² + y_w. 1. W = (−1, 3), A = (−6, 13)

	2
13 = a(−6 + 1)2 + 3 ⇔ 13 = 25a + 3 ⇒ 25a = 10 ⇒ a =
	5

	2
y =		(x + 1)2 + 3.
	5

2. W = (5, 0), A = (0, −100) dalej analogicznie do 1.

sushi_ gg6397228: bedzie "a" wyliczone i po zadaniu

kArOliNa: no ale wtedy wyjdzie 13/50 no nie?

kArOliNa: Bogdan a skąd wziąłeś to 25a ? mi ciągle wychodziło 47

sushi_ gg6397228: niee

Bogdan: obliczyłem: (−6 + 1)² = (−5)² = 25

sushi_ gg6397228: (−5)*(−5)=25

mila: Δ=b²−4ac 12a=4a²−4ac 12a=4a(a−c)/:4a 3=a−c c=a−3 teraz podstaw do punktu przez który przechodzi parabola czyli y=13 x=−6 y=ax²+bx+c b=2a 13=a*36−12a +a−3 teraz wyznacz z tego a podstaw je póżniej do wzoru który podałam ugóry na postać kanoniczna podstaw p iq i będzie gotowe przepraszam ale musze kończyć

Bogdan: mila po co wyznaczasz Δ?, nie utrudniaj łatwego rozwiązania.

kArOliNa: bogdan a to czasem nie wzór skróconego mnożenia ma być?

kArOliNa: to raczej ma być wzór skróconego mnożenia chyba

Bogdan: Zadanie 1 rozwiązałem. Nic więcej nie ma w tym rozwiązaniu do dodania. W podobny sposób trzeba rozwiązać zadanie 2.

kArOliNa: a no dobra dzięki

kArOliNa: nie czepiam się

sushi_ gg6397228: (−6+1)²= 36−12+1=25 −−> jak sie juz upierasz na wzorze skroconego mnozenia

kArOliNa: dobra dzięki wielkie

Gustlik: WYZNACZ WZÓR FUNKCJI KWADRATOWEJ W POSTACI KANONICZNEJ kArOliNa: 1.wyznacz wzór funkcji kwadratowej w postaci kanonicznej wiedząc że wierzchołkiem tej paraboli jest punkt W(−1,3) i do wykresu tej funkcji należy również punkt A(−6,13) Ad 1) W(−1,3) → p=−1, q=3 Postać kanoniczna wyglada tak: y=a(x+1)²+3 Podstawiasz teraz współrzędne A(−6,13) 13=a(−6+1)²+3 13=a*(−5)²+3 13=25a+3 13−3=25a 10=25a /:25

	10		2
a=		=
	25		5

	2
Odp: y=		(x+1)2+3
	5

ad. 2.wyznacz wzór funkcji kwadratowej w postaci kanonicznej jeśli największa wartością tej funkcji jest liczba zero osią symetrii jej wykresu jest prosta o równaniu x=5 i parabola tej funkcji przecina oś oy w punkcie A(0,−100) Największa wartość to q → q=0 Oś symetrii paraboli to prosta x=p → p=5 Zatem postać kanoniczna wyglada tak: y=a(x−5)²+0=a(x−5)² −100=a*(0−5)² −100=25a /:25 a=−4 Odp: y=−4(x−5)²