Witam :] Maciek: Przepraszam za brak polskich znakow 1.Funkcja g(x)=a^x , gdzie a jest rozwiazaniem rownania 16x²−33x+2=0,jest malejaca.Oblicz g(−0.25). 2.Dla jakich wartosci parametru k dane rownanie ma jedno rozwiazanie? I3^x−1I=k 3.Wyznacz zbior wartosci funkcji f(x)=25^x−10*5^x+9 Dziekuje za pomoc Mam male problemy z klawiatura. Nie chodzi o alt z shiftem.

think: 1. a jest rozwiązaniem równania: 16x² − 33x + 2 = 0 Δ = 961 √Δ = 31

	33 + 31
x1 =		= 2
	32

	33 − 31		1
x2 =		=
	32		16

	1
ponieważ g(x) jest malejąca to a∊(0,1) także 2 odpada i a =
	16

	1
g(x) = (		)x
	16

musisz tylko policzyć

	1		1
g(−		) = (		)−1/4 = ...
	4		16

2. ponieważ wartość bezwzględna przyjmuje tylko wartości dodatnie to dla k > 0 ma po dwa rozwiązania, dla k = 0 ma jedno rozwiązanie i dla k < 0 nie ma rozwiązania.

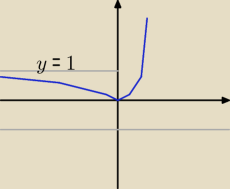
Bogdan: Szkic do zadania 2.

think: 3. f'(x) = 25^xln25 − 5^x*10ln5 = 0 5^x(5^xln25 − 5ln25) = 0 ⇒ 5^xln25 = 5ln25 ⇒ 5^x = 5 ⇒ x = 1 f(0) = 1 − 10 + 9 = 0 f(1) = 25 − 50 + 9 = − 16 ← czyli to jest minimum zatem funkcja osiąga wartości <−16,∞)

Gustlik: Ad 3) Można to zrobić bez pochodnych, bo w LO na ogół pochodnych już nie ma: f(x)=25^x−10*5^x+9 t=5^x>0 f(t)=t²−10t+9

	−b		10
t=p=		=		=5 >0 (spełnia założenie)
	2a		2

q=f(5)=5²−10*5+9=25−50+9=−16 ZW=<−16, +∞)

Tomasz: Zad. 1. g(x) = 2^−4x Zad 2. Dwa rozwiązania są dla 0 < k < 1. Jedno rozwiązanie jest dla k = 0 lub dla k ≥ 1. Zad 3. Trzeba wyznaczyć zbiór wartości funkcji bez wyznaczania pochodnych, tak, jak zrobił Gustlik.

think: Tomasz racja w ty drugim zrobiłam błąd, moje niedopatrzenie...

bibi: a brak w LO uważam osobiście za jakąś niedorzeczność

bibi: oczywiście miałem na myśli brak w LO pochodnych

wojtek: odkopuję. nie rozumiem rozwiązania Gustlika, chociaż pewnie jest najprostsze z możliwych. p i q to współrzędne wierzchołka funkcji kw. f(t), a wierzchołek ten leży na poziomej asymptocie funkcji wykładniczej f(x)? Dlaczego −16 również należy do zb. wartości?