proszę bardzo o pomoc.
Aga: w graniastosłupie prawidłowym czworokątnym dł krawędzi podstawy jest równa 8 cm. Oblicz Pc i V
tego graniastosłupa ,jeżeli przekątna tej bryły jest nachylona do płaszczyzny podstawy pod
kątem 60 stopni
15 wrz 20:59
terminex: która to klasa?
15 wrz 21:03
terminex: masz dwie opcje, związki miarowe albo trygonometria?
15 wrz 21:04
Aga: 3 gim
15 wrz 21:04
Lilija: Podstawa jest kwadratem, zatem można policzyć przekątną podst. z tw. Pitagorasa (d =
√128 =
8
√2). Z własności trójkąta równobocznego obliczasz wysokość graniastosłupa.
15 wrz 21:04
terminex: już pomagam
15 wrz 21:04
terminex: dobrze mówi
15 wrz 21:05
Lilija:
15 wrz 21:09
terminex:
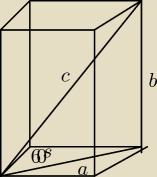
a już mamy dobrze podpowiedział 8
√2, c jest równe 16
√2, ponieważ przeciwprostokątna jest
dwa razy dłuższa od krótszej przyprostokątnej
a
2+b
2=c
2
(8
√2)
2+b
2=(16
√2)
2
128+b
2=512
b
2=384
b=
√384=8
√6
P
c=P
p+P
b
P
c=8cm
2+4*8cm*8
√6cm=64cm
2+256
√6=64(1+4
√6) cm
2
15 wrz 21:17
terminex: już objętość
V= Pp*h
V=8cm2*8√6 cm=512√6 cm3
Odp: Pole całkowite tego graniastosłupa wynosi 64(1+4√6) cm2, a objętość 512√6 cm3
15 wrz 21:20
terminex: proszę o pytania jak coś jest niezrozumiałe
15 wrz 21:20
terminex: tam przy objętości powinno być
V= (8cm)2*8√6 cm⇒64cm2*8√6=512√6 cm3
15 wrz 21:22
Filip: pole podstawy jest równe 8 cm2?
15 wrz 21:25
cerebot: miało być w nawiasie
15 wrz 21:29
cerebot: jako (8 cm)2
15 wrz 21:29
Kasia: a przypadkiem Pc=2Pp * Pb.?
15 wrz 21:31
terminex: Pc= 2Pp+Pp=2*64 cm2+4*8cm*8√6cm=128 cm2+256√6cm2=128(1+2√6) cm2
V=2Pp*h=2*64 cm2*8√6=1024√6 cm3
15 wrz 21:36
Filip: ale V już się liczy V=Pp*h.
15 wrz 21:39
Filip: a ile jest 8* 8√6?
15 wrz 21:51