Sprawdzić monotoniczność i ekstrema funkcji: e^(-2x^2) Emil: Bardzo prosiłbym o wyliczenie tego zadania...Znalezienie pochodnej nie jest problemem, natomiast dalsza część zadania owszem Sprawdzić monotoniczność i ekstrema funkcji: e^−2x2

Emil: Generalnie pochodna wyszła mi: −4e^−2x2

sushi_ gg6397228: 1. liczysz pochodna 2. f' =0 szukasz miesjc zerowych f' >0 to f rosnaca f'<0 to f malejaca jezeli w otoczeniu punktu( miesjca zerowego) nastepuje zmiana znaku to masz ekstremum − na + to minumum + na − to maksimum

sushi_ gg6397228: pochodna masz od funkcji zlozonej, wiec jest źle policzona

Emil: dobrze mam policzoną tylko połknąłem X −4xe^−2x2

Emil: i wychodzi na to że f`=0 ⇔ x=0 Co w takiej sytuacji? czy jestem w błędzie?

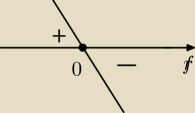
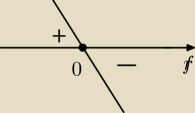sushi_ gg6397228: widac ze dla x<0 jest pochodna dodatnia, potem przechodzi na ujemna zmiana znaku z+ na − daje w punkcie 0 MAKSIMUM funckja rosnie dla x<0 funkcja maleja dla x>0