Beżowy: Prosta równoległa do podstawy AB trójkąta ABC, przecinająca ramiona AC i BC odpowiednio w punktach D i E, dzieli ten trójkąt na dwie fugury o równych polach. Oblicz stosunek długosci odcinków na które ta prosta dzieli ramiona trójkąta.

Beżowy: Bardzo proszę kogoś o pomoc. Błagam już Was od 16. Chciałbym wreszcie skończyć to zadanie.

Beżowy: Pomoże ktos?

Svanar: pisałem już: skorzystaj z podobieństwa figur/skali

Beżowy: No, ale nie potrafię Gdybym umiał to bym go rozwiązał... Możesz go zacząć?

Beżowy: Eta? Proszę..

Beżowy: halo?

Godzio:

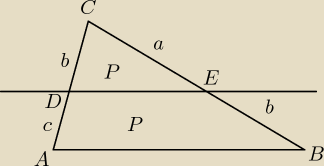
	a		b
Szukane:		,
	b		c

skala podobieństwa:

P
	= k2
P1

P
	= k2
2P

√2
	= k
2

a
	= k
a + b

	√2		√2
a =		a +		b
	2		2

	√2		√2
a(1 −		) =		b
	2		2

a		√2		2√2 − 2
	=		=		= √2 − 1
b		2 − √2		2

a
	= √2 − 1
b

	b
dokończ sam
	c

Beżowy: Niestety, nie rozumiem skąd Ci się to nabrało wszystko. Dało by radę to wytłumaczyć?

Godzio: Tak, poczekaj moment

Beżowy: Okej

Godzio:

	b		d
Jeszcze na początek napiszę że omyłkowo napisałem		tam powinno być
	c		c

i na rysunku tak samo d

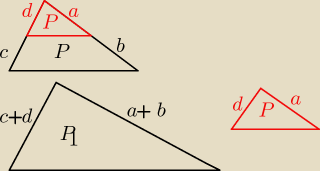Godzio: P₁ = 2P mamy 2 trójkąty podobne do siebie, możemy obliczyć skalę podobieństwa

P
	= k2
P1

P
	= k2
2P

1
	= k2
2

	1		√2
k =		=
	√2		2

	√2
Zatem trójkąty są podobne w skali k =		⇒ ich boki są w takim samym stosunku do
	2

siebie:

a
	= k
a + b

więc:

	√2
a =		(a + b) /*2
	2

2a = √2a + √2b 2a − √2a = √2b a(2 − √2) = √2b /: (2 − √2) / : b

a		√2
	=		−− rozszerzam ułamek
b		2 − √2

a		2√2 − 2
	=		= √2 − 1
b		2

więc stosunek tych odcinków jest równy:

a		d
	= √2 − 1 i w takim samym stosunku są
b		c

Beżowy: Powiedz mi jeszcze tak: 1. k² ? A czemu nie samo k?

	√2
2. Skąd się wzięło		? z rozszerzenia mianownika? (usunięcie niewymierności?)
	2

3. Wynik powinien być 1+√2 , pewnie gdzieś masz błąd obliczeniowy. Postaram się sam go znaleźć.

	d
4. Powiedz mi jeszcze na jakiej podstawie twierdzisz, że		mają ten sam stosunek? Z czego
	c

to wiadomo?

Godzio: 1. stosunek pól jest k² stosunek boków k stosunek objętności k³ i tak już jest 2. tak jak napisałeś

	√2		2√2 + 2
3. poprawka oczywiscie;		=		= √2 + 1
	2 − √2		2

	d
4. Tak to jest wszystkie boki są podobne w tej samej skali do siebie więc czy weźmiesz
	c

	a
czy		to i tak wyjdzie to sam możesz sprawdzić rozwiązaując analogicznie
	b

Beżowy: okej, dziękuję Ci za pomoc

Beżowy: Wszystko "gra i buczy"

Godzio: