? a: Trapez ABCD przedstawiony na rysunku jest rownoramienny. ile wynosi pole trapezu?

Kejt: dorysuj wysokość.. następnie oblicz ją z: https://matematykaszkolna.pl/strona/2280.html

a: dziekuje za pomoc a przede wszystkim za cierpliwosc

szus: moglby ktos dokladnie rozpisac jak zrobic tego typu zadanie? bo mam cos w tym sttylu ale w ogole nie mam pojecia jak sie za to zabrac

aa: moze ktos to obliczyc? bo za zadne skarby nie mozemy sie polapac o co chodzi

sushi_ gg6397228: opuść z wierzcholka C wysokosc na podstawe AB i masz trokat prostokatny CEA

	(|AB| +|CD|) * |CE|		2(|AE|) * |CE|
pole trapezu=		=
	2		2

sushi_ gg6397228: jak opusci sie wysokosc z D to bedzie punkt F |AB|= |AF| +|FE| + |EB| |CD| = |FE| |AF| + |FE| = |AE| a boki |CE| i |AF| policzysz z podpowiedzi KEJT

aa: ale jak mam obliczyc ile wynosi np AE?

bibi:

h		√2
	= sin45 ⇒ h = 16 *		= 8√2
16		2

Rysując wysokość z wierzchołka C na podstawę AB, tworzy się Δ prostokątny, a stąd kątg przy wierzchołku C ma miarę 45 stopni, a stąd dalej widać, że ten Δ jest równoramienny. Przyjmując: |AB| = |CD| + 2x z powyższego mamy: |CD| + x = h = 8√2

	|AB| + |CD|		|CD| + 2x + |CD|		2(|CD| + x)
P =		h =		h =		h = (|CD| + x) h
	2		2		2

Ostatecznie: P = 8√2 * 8 √2 = 64 * 2 = 128

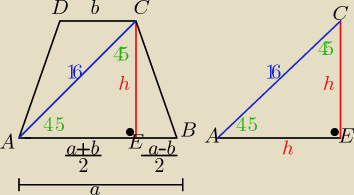
Eta: Trapez jest równoramienny, to : IEBI= ^a−b₂ to: IAEI= ^a+b₂ Δ AEC jest prostokątny i równoramienny => IAEI= ICEI= h

	a+b
IAEI=		= h
	2

	a+b
zatem P=		*h= h*h= h2
	2

P= h² z ΔAEC : h²+h²= 16² => 2h²= 256 => h²= 128 to: P= 128 [j²]