funkcja wykładnicza- pomóżcie patka: Zbadaj liczbę rozwiązań równania w zależności od parametru m 3^{|x−1|−|x|}=m

patka: proszę o pomoc

patka: pomóżcie mi proooooszę bo nie wiem jak to zrobić − PROSZĘ

patka: Wiem, że sobota i festiwal w Opolu ... ale może ktoś by mi pomógł przy tym zadanku

Godzio: umiesz chociaż narysować wykres f(x) = 3^{|x − 1| − |x|} ?

patka: Zbadać umiem tylko wykres nie wiem jakie przekształcenia wykonać

patka: Godzio, jakie przekształcenia wykonać?

Godzio: rozpisz przedziałami: 1^o x∊(−∞,0) 2^o x∊<0,1) 3^o x∊<1,∞) i w tych przedziałach rysuj części wykresu Rozpiszę Ci pierwszy 1^o x∊(−∞,0) ⇒ |x − 1| = −x + 1 , |x| = −x y = 3^{−2x + 1} dla x∊(−∞,0) podstawiaj punkty i rysuj wykres ale tylko w tym przedziale, inne analogicznie jak nie dasz rady to pisz

patka: ...analizuję to co mi napisałeś...

patka: Godzio, a czy dla przedziału 0, 1 otrzymamy y=3⁻2x+1?

Godzio: 2^o x∊<0,1) ⇒ |x − 1| = −x + 1, |x| = x y = 3 dla x∊<0,1)

Godzio: w tym przedziale wyrazenie pod pierwszą bezwzględnością jest zawsze ujemne dlatego trzeba zmienic znaki a pod drugą jest zawsze dodatnie wiec nie trzeba zmieniac znaku

patka: tzn y=3^−2x+1

patka: ale przed modułem w wykładniku jest minus więc chyba trzeba zmienić znaki...?

Godzio: a tak to w takim razie ja się walnąłem masz dobrze I w 1^o x∊(−∞,0) ⇒ |x − 1| = −x + 1 , |x| = −x więc y = 3 dla x∊(−∞,0) zapomniałem o tym −

patka: Godzio, dla pierwszego przypadku y=3 dla drugiego y=3^−2x+1 a dla trzeciego y=1/3 ?

Godzio: tak

patka: ... to dziękuję ci baaardzo − narazie

Godzio: No narazie i powodzenia

patka: Wszystko się zgadza, narysowałam wykres i z wykresu odczytałam rozwiązania. Jeszcze raz dzięki Godzio, pokazałeś mi kierunek działania

Godzio: To się cieszę że coś daje moja pomoc

patka: Godzio, mam do ciebie jeszcze jedno pytanie: jak rozwiązać graficznie (y+1/2x−3)(y−3)=0

Etyk: wykres funkcji z nawiasów narysuj ich przecięcie to rozwiązanie

patka: ahaaaa ok biorę się do pracy

Godzio: Pierwszy raz spotykam się z tego typu zadaniem i szczerze to głowy nie dam że to jest dobrze: narysuj 2 proste

	1
y = −		x + 3 i y = 3
	2

punkt ich przecięcia to rozwiązanie − ale naprawdę nie mam pojęcia czy to tak ma być

Eta: Co Godzio odpowie ...na to? ( 2, 1) ( (−4, 7) ( 150, −72) ........ ( 0,3) ( 5,3) ( −120,3) .........

patka: ...chyba właśnie tak − tak własnie zrobiłam

patka: Oczywiście odpowiadałam Godziowi

Eta: Sorry pierwszy punkt , to oczywiście: ( 2, 2) ( chochlik ....

patka: Już rozwiązałam chodziło o te dwie proste a nie o punkt przecięcia jaki tworzą więc nie jest potrzebny punkt przecięcia − Dzięki

Godzio: hmmm nie mam pojęcia o co chodzi

Godzio: rozumiem że te po prawej to są punkty pierwszego wykresu po lewej drugiego ale co z nimi ?

Eta: ok

patka: Godziu, bo jest dalsza część zadania, którą potrafiłam już wykonać

Eta: Rozwiązaniem są wszystkie punkty należące do obydwu prostych

patka: chodziło mi tylko o rozwiązanie jednego równania z układu równań

Godzio: aha to o to chodziło czyli jednym słowem to rozwiązaniem są te proste

patka: Właśnie tak jak mówi Eta

Eta:

patka: Dziękuję za pomoc Wynik zgadadza się z odpowiedziami w podręczniku

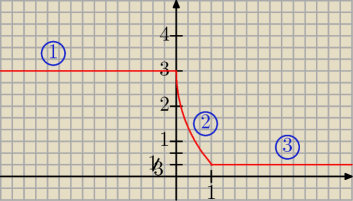
Bogdan: Dla x∊(−∞, 0): 3^{−x + 1 + x} = m ⇒ 3 = m Dla x∊<0, 1): 3^{−x + 1 − x} = m ⇒ 3^{−2x + 1} = m Dla x∊<1, +∞): 3^{x − 1 − x} = m ⇒ 3⁻¹ = m Linia 1: y = 3 Linia 2: y = 3^{−2x + 1}

	1
Linia 3: y = 3−1 ⇒ y =
	3

Linia y = m jest funkcją stałą. Równanie ma:

	1
* brak rozwiązań dla m∊(−∞,		)∪(3, +∞)
	3

	1
* 1 rozwiązanie dla m∊(		, 3)
	3

	1
* nieskończenie wiele rozwiązań dla m =		lub m = 3
	3

patka: Napracowałeś się Bogdan rozwiązanie dokładnie takie samo jak moje