ciąg arytmetyczny czekolada: Udowodnij,że jeśli trzy kolejne kąty czworokąta wpisanego w koło tworzą ciąg arytmetyczny, to co najmniej dwa kąty tego czworokąta są proste. nie wiem.. jakieś wskazówki chociaż..

Bogdan: Kiedy czworokąt można wpisać w koło? Zacytuj twierdzenie o czworokącie wpisanym w koło.

czekolada: katy przeciwlegle w czworokacie wpisanym w okrag maja razem 180^o

Godzio: α,β,γ,δ −−− kąty czworokąta => α + γ = β + δ = 180^o α,β,γ −−− ciąg arytmetyczny gdzie α + γ = 180^o Skorzystaj z zależności ciągu arytmetycznego i to prawie będzie koniec

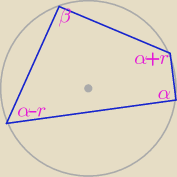
Bogdan: No właśnie, czyli uwzględniając warunki zadania otrzymujemy: (α − r) + (α + r) = 180^o oraz α + β = 180^o Z pierwszego równania oblicz α, z drugiego β

czekolada: α i β maja po 90^o ale mialo wyjsc,ze co najmniej trzy katy mają po 90^o , a nie jestesmy chyba w stanie obliczyć ile ma r. chyba,ze jest tez tak ze α+ α+r = 180^o, bo są przy jednej scianie.. ja znam tylko tą własnąć,że kąty przeciwkległe mają po dodaniu 180^o

czekolada: ok, tamte pozostałe dwa muszą być też kątami prostymi siłą rzeczy tylko jak to zapisać ?

Bogdan: Przypominam treść zadania: Udowodnij, że jeśli trzy kolejne kąty czworokąta wpisanego w koło tworzą ciąg arytmetyczny, to co najmniej dwa kąty tego czworokąta są proste. Czyli dwa lub więcej kątów ma miarę 90^o. Dwa już są, to kąty α i β. Dla jakich wartości r pozostałe kąty też będą proste?

czekolada: dla r=0

czekolada: czyli to bedzie udowodnione jesli obliczylam α i β, tak ? i np. na maturze nie muszę już nic wiecej pisac ?

Bogdan: Tak, dowód jest przeprowadzony. Należałoby jeszcze napisać na końcu zdanie: co należało udowodnić.

czekolada: ok, dziekuje

Bogdan: Nie było takie trudne, prawda?

czekolada: no nie było, ale czasami trudno jest dobrze zapisać wszystkie dane