Marcin: Uprzejmie proszę o rozwiązanie kilku zadanek dla mojej mamy. Sam ich nie potrafie a jej są potrzebne. Z góry bardzo dziękuję! Z.1 Wiedząc, że liczba 1 jest pierwiastkiem wielomianu W(x)=x³ + 3x² - 5x + 1 znajdź pozostałe pierwiastki tego wielomianu. Z.2 Dla jakich wartości parametru a liczba 2 jest pierwiastkiem wielomianu W(x)=x³ + 2ax² - 3ax + 4 z.3 Rozwiąż równania i nierówności: a) x³ + 3x² - 4x -12=0 b)x³ + 5x² - 6x > 0 c) x³ - 4x< 0 d)[ułamek] x+9/x+2 = x-3 e) [ułamek] x-3/x+2 <5

Eaniel: Z.1 Skoro 1 jest pierwiastkiem, to znaczy że wielomian dzieli się bez reszty przez (x-1) podziel sobie ten wielomian przez (x-1), żeby otrzymać: W(x)=(x-1)(x²+4x-1) (możesz dzielić pisemnie, albo korzystać z tzw. Tabelki Hornera). Pozostałe pierwiastki znajdziesz w wyłączonym trójmianie, czyli normalnie jak z równaniem kwadratowym - liczysz deltę i pierwiastki. Δ=16-4*(1*(-1))=16+4=20 √Δ=√20=2*√5 x₁=(-4-2*√5)/2=-2-√5 x₂=(-4+2*√5)/2=-2+√5

Gwiazdka: Z przyjemnością! 1/ należy wykonać dzielenie W(x) przez x-1 ( x³ +3x² -5x +1) x-1) = x² +4x - 1 - x³ +x² ------------- = 4x² -5x -4x² +4x ------------ = - x +1 +x - 1 ---------- = = zatem mamy rozkład W(x) na czynniki (x-1)(x² +4x - 1) dla wyrażenia w drugim nawiasie obliczamy Δ= 16 +4 = 20 √Δ = p{20] = 2p{5] - 4 +2√5 - 4 - 2√5 x₁ = ----------- x₂ = ------------- 2 2 x₁ = -2 + √5 x₂ = - 2 - √5 ---- to są te pieriastki 2/ 2 -- jest pierwiastkiem wielomianu to oznacza,że W(2) =0 zatem W(2)= 2³ +2*a*2² - 3*a*2 +4= 8 +8a -6a = 2a+8 więc 2a +8= 0 2a = - 8 a = - 4 odp; dla a = - 4 3/ a) grupujemy pierwsze dwa wyrazy i pozostałe x²(x+3) -4(x+3) =0 (x+3)( x² - 4)=0 (x+3)(x-2)(x+2) =0 więc x₁= - 3 x₂ = 2 x₃= - 2 b) x(x² +5x - 6) >0 Δ=25 +24=49 √Δ=7 x= 0 lub x= (- 5+7)/2 lub x= ( - 5 - 7)/2 x=0 lub x =1 lub x = - 6 rys. pomocniczy --------------------- -------------------- /+ + + + + / / + + + + --------- -6 /------------------- /0---------- 1/------------------------> x - - - / / - - - - / --------------- /------------/ wybieramy wart. dodatnie czyli odp; xE (- 6, 0) U ( 1, ∞) c) x(x² - 4) <0 x(x -2)(x+2) <0 x = 0 x = 2 x = - 2 narysować podobny rysunek przez miejsca od prawej strony - 2 , 0 , 2 wybrać te z pod osi ( czyli ujemne) odp:xE(-∞, - 2) U ( 0, 2) d) dziedzina równania: D= R - {-2} x +9 (x - 3)(x+2) ------------- - ------------ = 0 <=> x +9 - x² +x +6=0 x +2 x +2 - x² +2x +15=0 Δ= 4 +60 = 64 √Δ=8 x₁=(-2 +8)/ -2 x₂ = (-2 -8)/ -2 x₁= - 3 x₂= 5 odp; x = - 3 , x = 5 e) podobnie D = R -{ -2} x - 3 5 (x+2) ------------ - ---------- <0 x +2 x +2 x - 3 -5x -10 - 4x - 13 ----------------- <0 to ------------- < 0 x +2 x + 2 czyli (x+2)( - 4x - 13) <0 <=> (x+2)( 4x+13) >0 ( zmiana zwrotu nier.) x= - 2 x = - 13/4 odp; xE (-∞, - 13/4) U ( - 2 ,∞)

Gwiazdka: Tam gdzie wyskoczył "ufoludek" ma być znak dzielenia

Mariusz: Witam, a czy ja mógłbym prosić o pomoc z podobnym zadaniem? Próbowałem na podstawie przykładu wyżej..ale to dzielenie w słupku coś mi nie wychodzi 1) Wiedząc że liczba 3 jest pierwiastkiem wielomianu W(x)=x³ − 2x² − 8x + a wyznacz a 2) Rozwiąż równania i nierówności x³ − 8x = 0 x³ + 6x² − 4x −24 = 0

6 − x
	= 3
5x

x − 1		x + 2
	=
x + 2		x −1

(x − 7)² (x − 3)(1 − x) ≥ 0 Dziękuję z góry i pozdrawiam

;): 1) W(3) = 0 27 − 18 − 24 + a = 0 a = ? 2) a) x(x + 2√2)(x − 2√2) = 0 b) x²(x + 6) − 4(x + 6) = 0 (x + 6)(x + 2)(x − 2) = 0 c) D = R \ {0} 6x = 6 x = ? d) D = R \ {−2,1} (x − 1)² = (x + 2)² x² − 2x + 1 = x² + 4x + 4 6x = −3 x = ? e) x∊<1,3>∪{7}

Gustlik: Z.1 Wiedząc, że liczba 1 jest pierwiastkiem wielomianu W(x)=x³ + 3x² − 5x + 1 znajdź pozostałe pierwiastki tego wielomianu. Schemat Hornera: 1 3 −5 1 1 1 4 −1 0 (x−1)(x²+4x−1)=0 x=1 lub Δ=4²−4¹*(−1)=16+4=20 √Δ=√20=2√5 x₁=U{−4−2√5]{2}=−2−√5 x₂=−2+√5 Z.2 Dla jakich wartości parametru a liczba 2 jest pierwiastkiem wielomianu W(x)=x³ + 2ax² − 3ax + 4 W(2)=2³+2a*2²−3a*2+4=8+8a−6a+4=2a+12 2a+12=0 2a=−12 /:2 a=−6 z.3 Rozwiąż równania i nierówności: a) x³ + 3x² − 4x −12=0 x²(x+3)−4(x+3)=0 (x²−4)(x+3)=0 (x−2)(x+2)(x+3)=0 x=2 v x=−2 v x=−3 b)x³ + 5x² − 6x > 0 x(x²+5x+6)>0 x=0 lub Δ=25−4*1*6=25−24=1 √Δ=1

	−5−1
x1=		=−3
	2

	−5+1
x2=		=−2
	2

c) x³ − 4x< 0 dalej wg wskazówek Gwiazdki d)[ułamek]

x+9
	= x−3 /*(x+2) − przy równaniach nie trzeba sprowadzać do wspólnego mianownika,
x+2

tylko wymnożyć obustronnie przez wspólny mianownik − jest prościej. D=R−{−2} dziedzina równania x+9=(x−3)(x+2) x+9=x*2+2x−3x−6 0=x²−2x−15 x²−2x−15=0 Δ=(−2)²−4*1*(−15)=4+60=64 √Δ=8

	2−8		−6
x1=		=		=−3
	2		2

	2+8		10
x2=		=		=5 → oba należą do dziedziny.
	2		2

e) [ułamek] x−3/x+2 <5 wg wskazówek Gwiazdki

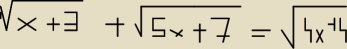Kasia: Pomóżcie Mi to rozwiązac

ICSP: √x+3 + √5x+7 = √4x + 4

Kasia: tak

ICSP: mi to wygląda na brak rozwiązań, ale pewien nie jestem.

Kasia: hmm..sama nie wiem nawet jak sie zabrac za to zadanie

ICSP: Zrobię na spokojnie jak wrócę − za około półtorej godziny.

Mateusz: Kasia po 1) na przyszłosc zakładaj osobny wątek 2) załoz najpierw załozenia x+3≥0 5x+7≥0 i 4x+4≥0 teraz podnies rownanie do kwadratu obustronnie i rozwiąż tylko uwaga czasami moze zdarzyc sie tzw obcy pierwiastek czyli taki ktory nie spełnia równania dzieje się tak dlatego ze nie zawsze podnoszenie do kwadratu powoduje otrzymanie równania równoważnego wiec jedyny sposob zeby taki pierwiastek wyłapac to podstawienie do wyjsciowego rownania podam ci na innym przykładzie: √x+4=x−2 √x+4=x−2/² (√x+4)²=(x−2)² x+4=x²−4x+4=> x²−5x=0, x(x−5)=0 czyli x=0 v x=5 i po podstawieniu do wyjsciowego rownania widac ze 0 nie spełnia go

Kasia: dziękuje bardzo !

Piotr: a oto co wymyslil wolfram http://www.wolframalpha.com/input/?i=sqrt%28x%2B3%29+%2B+sqrt%285x%2B7%29+%3D+sqrt%284x+%2B+4%29++

pigor: ... no to zobaczmy np. tak : dziedzina D_r = {x∊R: x+3≥0 i 5x+7≥0 i 4x+4≥0} ⇒ x≥−3 i x≥−1,4 i x≥−1 ⇒ D_r= [−1;+∞) , a w niej √x+3+√5x+7= √4x + 4 /² ⇔ x+3+2√(x+3)(5x+7)+5x+7= 4x+4 ⇔ ⇔ 2√(x+3)(5x+7)= −2x−6 / : 2 ⇔ √(x+3)(5x+7)= −x−3 , ale −x−3≥0 i x≥−1 z D_r ⇔ x≤−3 i x≥−1 ⇔ x∊∅ , zatem dane równanie jest sprzeczne . ...

Justyna. : 1.Dany jest wielomian w(x)= 2x⁴+x³−8x²−x+6 a) . znajdź pierwiastek wielomianu 2. Rozwiąż równania a). x³−16x=0 b). x³−x²+8x−8=0 c). x³−5x²−2x+10=0

Justyna. : Proszę o pomoc w rozwiązaniu tych zadań . Z góry dziękuję .

Piotr: Dodaj nowe zadanie !

Basia: Mateusz przykład, który podajesz nie przystaje do zadania Kasi w równaniu √x+3 + √5x+7 = √4x + 4 obie strony są nieujemne i wobec tego po podniesieniu do ()² dostajesz równanie równoważne oczywiście najpierw założenia x≥ −3 i x≥ −⁷₅ i x≥ − 1 ⇒ x≥ −1 x+3 + 2√(x+3)(5x+7) + 5x + 7 = 4x + 4 2√(x+3)(5x+7) = −2x − 6 :2 √(x+3)(5x+7) = −x−3 dla −x−3<0 czyli dla x>−3 nie ma rozwiązania bo (lewa dodatnia) ≠ (prawej ujemnej) czyli musiałoby być x≤ −3 i koniec zabawy, bo to jest sprzeczne z założeniem

xyz: Wyznacz zbiór liczb, które spełniają obie nierówności: 3x +2> 0 i 2 + x ≥ 5.

aśku: Dla jakiej wartości parametru a∈R wielomian W(x) = x13+3x+ a dzieli się bez reszty przez x+1 ? z góry dziękuję

krystek: W(−1)=0 podstaw za x=−1 i wylicz a